رئيس الوزراء أرقام والأرقام المركبة

رئيس الوزراء أرقام والأرقام المركبة

رئيس وعدد ويمكن تقسيم بالتساوي فقط بنسبة 1 أو نفسها.
ويجب أن يكون عدد صحيح أكبر من 1.

على سبيل المثال: 7 لا يمكن إلا أن تكون مقسمة بالتساوي بنسبة 1 أو 7، لذلك هو عدد أولي.

ولكن 6 يمكن تقسيمها بالتساوي من 1 و 2 و 3 و 6 لذلك هو ليس عددا أوليا (وهو مركب رقم).

دعني أشرح ...

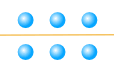
بعض أرقام كاملة ويمكن تقسيم تصل بالتساوي، وبعض لا!

مثال:

6 يمكن تقسيمها بالتساوي بنسبة 2، أو بنسبة 3:

6 = 2 × 3

مثله:

	أو
مقسمة إلى مجموعات 2		تقسيمها إلى 3 مجموعات

ولكن 7 لا يمكن قسمت بالتساوي:

ونقدم لهم أسماء:

عندما يمكن تقسيم عدد يصل بالتساوي بل هو عدد مركب
عندما يمكن لعدد لا تقسم بالتساوي حتى أنها برايم عدد

حتى 6 غير مركب، ولكن 7 هو رئيس.

وهذا ما يفسر ذلك ... ولكن هناك بعض مزيد من التفاصيل ...

ليس في الكسور

نحن نتعامل فقط مع الأعداد الصحيحة هنا! ونحن لن تقطع الأشياء الى نصفين أو أرباع.

ليس في المجموعات من 1

حسنا، نحن يمكن أن تنقسم إلى سبعة 7 1S (أو واحدة 7) من هذا القبيل:

7 = 1 × 7

ولكن يمكننا أن نفعل ذلك أي عدد صحيح!

لذلك ينبغي علينا أيضا أن نقول إننا لا نرغب في قسمة 1 ، أو عن طريق الرقم نفسه.

وهو رئيس الرقم عندما لا يمكن تقسيمها بالتساوي من قبل أي عدد
(باستثناء 1 أو نفسه).

على سبيل المثال: هو 7 رئيس ورقم أو عدد مركب؟

• ونحن لا يمكن تقسيم 7 بالتساوي بنسبة 2 (نحصل على 2 الكثير من 3، مع ترك واحدة فوق)
• ونحن لا يمكن تقسيم 7 بالتساوي بنسبة 3 (نحصل على 3 عقود من 2، مع ترك واحدة فوق)
• ونحن لا يمكن تقسيم 7 بالتساوي من قبل 4 أو 5 أو 6.

يمكننا فقط تقسيم 7 في مجموعة واحدة من 7 (أو سبع مجموعات من 1):

7 = 1 × 7

حتى 7 يمكن إلا أن تكون مقسمة بالتساوي بنسبة 1 أو نفسها :

حتى 7 هو عدد أولي

و أيضا:

وهو عدد مركب عندما يمكن تقسيمها بالتساوي
من قبل أعداد أخرى من 1 أو نفسها.

مثله:

على سبيل المثال: هو 6 رئيس ورقم أو عدد مركب؟

6 يمكن تقسيمها بالتساوي بنسبة 2، أو 3، فضلا عن 1 أو 6:

6 = 1 × 6
6 = 2 × 3

حتى 6 هو عدد مركب

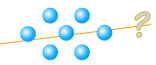
في بعض الأحيان عددا ويمكن تقسيم بالتساوي نواح كثيرة :

مثال: 12 ويمكن تقسيم بالتساوي بنسبة 1، 2، 3، 4، 6 و 12:

1 × 12 = 12
2 × 6 = 12
3 × 4 = 12

حتى 12 هو عدد مركب

ولاحظ هذا:

أي عدد صحيح أكبر من 1 إما رئيس أو المركب

ماذا عن 1؟

سنوات قبل 1 أدرج باعتباره رئيس، ولكن الآن ليس :

1 هو ليس رئيس وأيضا لا المركب .

العوامل

يمكننا أيضا تحديد رئيس وعدد باستخدام العوامل.

"عوامل" أرقام ضربنا
معا للحصول على رقم آخر.

ونحن لدينا:

عندما اثنين من العوامل الوحيدة من عدد و 1 ورقم ،
بعد ذلك هو عدد اولى

فهذا يعني أن نفس التعريف السابق، ذكر فقط باستخدام العوامل.

وتذكر هذه ليست سوى حوالي الأعداد الصحيحة (1، 2، 3، ... الخ)، وليس الكسور أو الأرقام السالبة. حتى لا أقول "أنا يمكن أن تتضاعف ½ مرات 6 للحصول على 3" OK؟

أمثلة:

3 = 1 × 3 (العوامل الوحيدة هي 1 و 3)	أولي
6 = 1 × 6   أو   6 = 2 × 3(العوامل هي 1،2،3 و 6)	مركب

أمثلة من 1-14

عوامل أخرى غير 1 أو رقم يتم نفسها سلط الضوء :

رقم	يمكن بالتساوي مقسمة بواسطة	رئيس الوزراء، أو المركب؟
1	(1 لا يعتبر رئيس الوزراء أو المركبة)
2	1، 2	أولي
3	1 و 3	أولي
4	1، 2 ، 4	مركب
5	15	أولي
6	1، 2 ، 3 ، 6	مركب
7	1، 7	أولي
8	1، 2 ، 4 ، 8	مركب
9	1، 3 ، 9	مركب
10	1، 2 ، 5 ، 10	مركب
11	1، 11	أولي
12	1، 2 ، 3 ، 4 ، 6 ، 12	مركب
13	1، 13	أولي
14	1، 2 ، 7 ، 14	مركب
...	...	...

حتى عندما تكون هناك المزيد من العوامل من 1 أو العدد نفسه، والرقم هو مركب .

سؤال لك: 15 رئيس أو المركب؟

لماذا كل هذه الضجة حول رئيس والمركب؟

لأننا لا نستطيع "تحطيم" الأرقام المركبة إلى عوامل عدد أولي.

هو مثل رئيس الأرقام هي اللبنات الأساسية لجميع الأرقام. ويتم إجراء أرقام المركبة تتألف من رئيس الأرقام تضاعفت معا.

وهنا نرى أنه في العمل:

2 هو رئيس (3)، رئيس الوزراء، 4 غير مركب (= 2 × 2) (5)، رئيس الوزراء، وهلم جرا ...

مثال: 12 يتم عن طريق ضرب الأعداد الأولية 2 ، 2 و 3 معا.

12 = 2 × 2 × 3

عدد 2 وتكرر، والتي على ما يرام.

في الواقع يمكن أن نكتب مثل هذا باستخدام الأس 2:

12 = 2 ² × 3

وهذا هو السبب في ما يطلق عليه " المركب أرقام" لمركب يعني "شيء مصنوع من خلال الجمع بين الأشياء"

هناك العديد من الألغاز في الرياضيات التي يمكن حلها بسهولة أكبر عندما كنا "تفريق" أرقام المركبة إلى عوامل عدد ريعان الشباب. ويستند الكثير من أمن الإنترنت في الرياضيات باستخدام الأعداد الأولية.