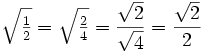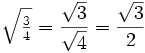وحدة الدائرة

"وحدة الدائرة" هو دائرة نصف قطرها 1.

كونها بسيطة جدا، بل هو وسيلة رائعة لتعلم والحديث عن الأطوال والزوايا.

يتم وضع مركز على الرسم البياني حيث المحور x و y عبر محور، حتى نحصل على هذا الترتيب أنيق هنا.

الجيب وجيب التمام والظل

لأن دائرة نصف قطرها 1، يمكننا قياس مباشرة الجيب وجيب التمام والظل .

ماذا يحدث عندما زاوية، θ، هو 0 °؟

كوس 0 ° = 1، والخطيئة 0 ° = 0 و تان 0 ° = 0

ماذا يحدث عندما θ هي 90 درجة؟

كوس 90 درجة = 0، والخطيئة 90 درجة = 1 وتأن 90 ° غير معرف

انها محاولة لنفسك!

جرب حظك! تحريك الماوس حوله ليرى مدى اختلاف الزوايا (في راديان أو درجة ) تؤثر على الجيب وجيب التمام والظل

و"الجانبين" يمكن أن تكون إيجابية أو سلبية وفقا لقواعد الإحداثيات الديكارتية . وهذا يجعل التغيير الجيب وجيب التمام والظل بين القيم الإيجابية والسلبية أيضا.

كما حاول التفاعلية وحدة الدائرة .

فيثاغورس

نظرية فيثاغورس " تقول أن لمثلث قائم الزاوية، مربع من الجانب الطويل يساوي مجموع مربعات من الجانبين الآخرين:

س ² + ص ² = 1 ²

ولكن 1 ² هو مجرد 1، لذلك:

س ² + ص ² = 1 
(على معادلة دائرة الوحدة)

أيضا، منذ س = جتا والخطيئة ص =، نحصل على:

(كوس (θ)) ² + (الخطيئة (θ)) ² = 1

مفيد "الهوية"

زوايا مهمة: 30 ° ، 45 ° و 60 °

يجب أن تحاول تذكر الخطيئة، كوس وتأن لزوايا 30 درجة ، 45 درجة و 60 درجة .

نعم، نعم، فمن ألم لدينا لتذكر الأشياء، ولكنه سيجعل الحياة أسهل عندما تعلم منهم، وليس فقط في الامتحانات، ولكن مرة أخرى عندما كنت في حاجة للقيام تقديرات سريعة، الخ

وهذه هي القيم التي ينبغي أن نتذكر!

زاوية	خطيئة	كوس	تان = سين / كوس
30 °			1 √3 = √3 3
45 °			1
60 °			√3

كيفية حفظ؟

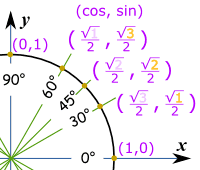
لمساعدتك على تذكر، والتفكير "1،2،3" :

	الخطيئة (30 درجة ) =	√ 1	=	1	(لأن √1 = 1)
		2		2

	الخطيئة (45 درجة ) =	√ 2
		2

	الخطيئة (60 درجة ) =	√ 3
		2

وكوس يذهب "3،2،1"

	كوس (30 درجة ) =	√ 3
		2

	كوس (45 درجة ) =	√ 2
		2

	كوس (60 درجة ) =	√ 1	=	1	(لأن √1 = 1)
		2		2

فقط 3 أرقام

في الواقع، مع العلم 3 أرقام غير كافية:	1	،	√2	و	√3
	2		2		2

لأنهم يعملون ل كوس فضلا عن الخطيئة :

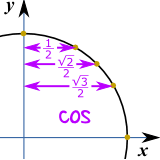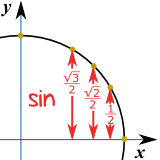ماذا عن تان؟

حسنا، تان = الخطيئة / جتا حتى نتمكن من حساب مثل هذا:

تان (30 درجة) = الخطيئة (30 درجة)  =  1/2  =  1 كوس (30 درجة) √3 / 2 √3		لكن الكتابة 1 / √3 قد يكلفك علامات (انظر مقامات الرشيد )، وذلك بدلا من استخدام √3 / 3
تان (45 درجة) = الخطيئة (45 درجة)  =  √2 / 2  = 1  كوس (45 درجة) √2 / 2
تان (60 درجة) = الخطيئة (60 درجة)  =  √3 / 2  = √3  كوس (60 درجة) 1/2

رسم سريعة

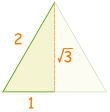
وهناك طريقة أخرى لمساعدتك على تذكر 30 ° و 60 ° هو جعل رسم سريع:

رسم مثلث مع أطوال الأضلاع من 2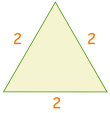
خفضت الى النصف. فيثاغورس يقول الجانب الجديد √3 1 2 + (√3) 2 = 2 2 1 + 3 = 4
ثم استخدم sohcahtoa عن الخطيئة، كوس أو تان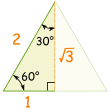

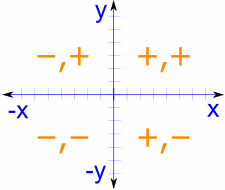
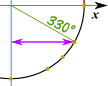
على سبيل المثال: الخطيئة (30 درجة)

شرط: سوه cahtoa

ينقسم شرط العكس من الوتر

الخطيئة (30 درجة) = المعاكس الوتر = 1 2

الدائرة الجامع

للدائرة كاملة نحتاج القيم في كل رباعي ، مع زائد الصحيحة أو علامة الطرح حسب الاحداثيات الديكارتية :

علما بأن كوس هي أولا و الخطيئة هي الثانية، لذلك يذهب (كوس، والخطيئة) :

حفظ ك PDF

على سبيل المثال: ما هو كوس (330 درجة)؟

جعل رسم مثل هذا، ويمكننا أن نرى ذلك هو قيمة "طويلة":	√3
	2

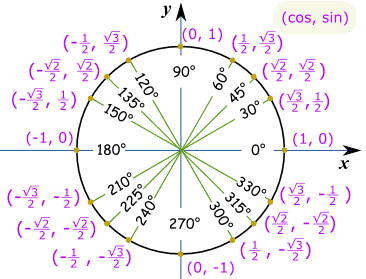
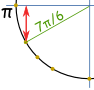
وهذا هو نفس الدائرة وحدة في راديان .

على سبيل المثال: ما هي خطيئة (7 π / 6)؟

التفكير "7 π / 6 = π + π / 6"، ثم جعل رسم.
بعد ذلك يمكننا أن نرى ذلك هو سلبي وغير قيمة "قصيرة": -½

السؤال 1 السؤال 2 السؤال 3 س 4 س 5 السؤال 6 السؤال 7 السؤال 8 السؤال 9 سؤال 10  

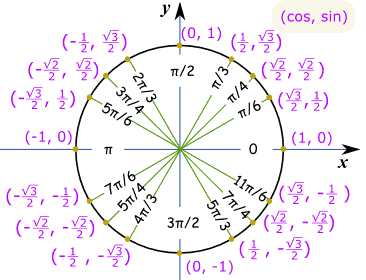
حاشية: أين القيم تأتي من؟ يمكننا استخدام المعادلة س 2 + ص 2 = 1 للعثور على أطوال س و ص (التي تساوي كوس و الخطيئة عندما نصف قطرها 1 ):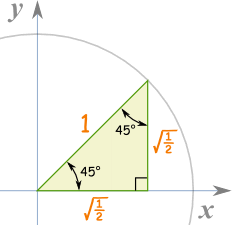 45 درجة 45 درجة، x و y وعلى قدم المساواة، لذلك ص = س : س 2 + س 2 = 1 2X 2 = 1 س 2 = ½ س = ص = √ (½) 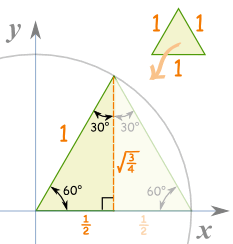60 درجة خذ مثلث متساوي الأضلاع (جميع الأطراف على قدم المساواة وجميع الزوايا و60 درجة) وتقسيمه عن طريق الوسط. الجانب "x" هو الآن ½ ، والجانب "ص" هو: (½) 2 + ص 2 = 1 ¼ + ص 2 = 1 ص 2 = 1 = ¼ ¾ ذ = √ (¾) 30 درجة 30 ° هو فقط 60 درجة مع x و y تبادلت، لذلك س = √ (¾) و ذ = ½ و: √ (½) هو أيضا هذا:   و√ (¾) هو أيضا هذا:   وهنا هو نتيجة (نفس كما في السابق): زاوية خطيئة كوس تان = سين / كوس 30 ° 1 √3 = √3 3 45 ° 1 60 ° √3