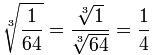الجذر النوني في الرياضيات

الجذر النوني  

• جذور "2ND" هو الجذر التربيعي
• جذور "3rd على" هو الجذر التكعيبي
• إلخ!

2				تماما مثل الجذر التربيعي يستخدم اثنين مرات في الضرب للحصول على القيمة الأصلية.
3				و الجذر التكعيبي يستخدم ثلاث مرات في الضرب للحصول على القيمة الأصلية.
...		...		...
ن				و جذر عدد يستخدم ن مرات في الضرب للحصول على القيمة الأصلية.

لذلك فإن العامة سيلة لنتحدث عن جذور
(لذلك يمكن أن يكون 2ND، أو 9TH، أو 324th، أو أيا كان)

الجذر رمز الألف

هذا هو رمز خاص وهذا يعني "جذر عدد"، هو "المتطرف" رمز (التي تستخدم لجذور مربع) مع قليل من ن على أنها تعني الألف الجذر.

استخدامه

يمكننا استخدام جذر عدد في سؤال مثل هذا:

سؤال: ما هو "ن" في هذه المعادلة؟

الجواب: أنا فقط أعلم أن 625 = 5 ⁴ ، وبالتالي فإن 4 يجب أن يكون الجذر ال 625 5:

أو يمكن أن نستخدمها "ن" لأننا نريد أن نقول الأشياء العامة:

مثال: عندما ن الغريب    (ونحن نتحدث عن ذلك لاحقا).

لماذا "الجذر" ...؟

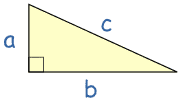
عندما ترى "الجذر" أعتقد واضاف "اعرف الشجرة ، ولكن ما هو الجذر الذي أنتج ذلك؟ " على سبيل المثال: في 9√ = 3 "شجرة" هو 9 ، والجذر هو 3 .

الخصائص

الآن نحن نعرف ما هو جذر عدد، دعونا نلقي نظرة على بعض الخصائص:

الضرب والقسمة

نستطيع "مزق" الضرب تحت علامة الجذر مثل هذا:

( إذا كانت n هي حتى، أ و ب ويجب أن يكون كل من ≥ 0)

هذا يمكن أن تساعدنا على تبسيط المعادلات في الجبر، وأيضا جعل بعض الحسابات أسهل:

مثال: 

كما أنها تعمل لتقسيم:

( a≥0 وب> 0)
(ب لا يمكن أن يكون صفرا، ونحن لا يمكن القسمة على صفر)

مثال:

جمع وطرح

لكننا لا يمكن أن تفعل هذا النوع من الشيء لإضافات أو الطرح!

مثال: نظرية فيثاغورس " تقول

و 2 + ب 2 = ج 2

حتى نتمكن من حساب ج من هذا القبيل:

ج = √ (أ ² + ب ² )

وهو ليس نفس ج = أ + ب ، أليس كذلك؟

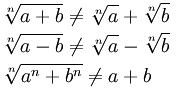وهو فخ السهل الوقوع، لذلك حذار. وهذا يعني أيضا أنه، للأسف، الإضافات والطرح يمكن أن يكون من الصعب التعامل مع عندما تحت علامة الجذر.

الأسس مقابل الجذور

داعية على جانب واحد من "=" يمكن أن تتحول إلى الجذر على الجانب الآخر من "=":

إذا      ثم      (عندما ن، بل هو يجب أن يكون ب ≥ 0)

مثال: