تبسيط الجذور التربيعية
تبسيط الجذور التربيعية
لتبسيط الجذر التربيعي: جعل عدد داخل الجذر التربيعي صغيرة قدر الإمكان (ولكن لا يزال عدد صحيح ):
حكم مفيدة لنتذكر عندما أ و ب ليست سلبية:
وهذا هو كيفية استخدامه:
هنا مثال آخر:
وهنا هو كيفية تبسيط في سطر واحد:
وغالبا ما يساعد على عامل الأرقام (في الأعداد الأولية الأفضل):
الكسور
هناك قاعدة مماثلة للكسور:
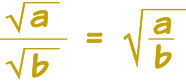
تبسيط الجذور التربيعية
![تبسيط الجذور التربيعية]() Reviewed by . blogmathappily
on
7:00 م
Rating:
Reviewed by . blogmathappily
on
7:00 م
Rating:
