الرسوم البيانية التربيعية المعادلات

A معادلة من الدرجة الثانية في نموذج عادي
( ل ، ب ، و ج يمكن أن يكون لها أي قيمة، إلا أن ل لا يمكن أن يكون 0.)

هنا مثال:

الرسوم البيانية

يمكنك الرسم البياني لمعادلة الدرجة الثانية باستخدام غرافر وظيفة ، ولكن ل نفهم حقا ما يجري، يمكنك جعل الرسم البياني نفسك. واصل القراءة!

وأبسط الدرجة الثانية

أبسط المعادلات التربيعية هي:

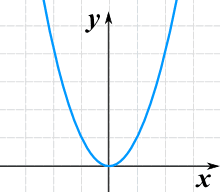
و (س) = س ²

والرسم البياني لها بسيط جدا:

هذا هو منحنى و (س) = س ²
وهو القطع المكافئ .

والآن دعونا نرى ما سيحدث عندما نقدم على "أ" القيمة:

و (س) = الفأس ²

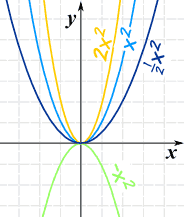
• قيم أكبر من و الاسكواش منحنى الداخل
• قيم أصغر من و توسيعه إلى الخارج
• والقيم السلبية على الوجه رأسا على عقب

العب به الآن هو الوقت المناسب للعب مع " الدرجة الثانية معادلة إكسبلورر " حتى تتمكن من معرفة ما قيم مختلفة ل ، ب و ج القيام به.

"اللواء" الدرجة الثانية

قبل الرسوم البيانية نحن إعادة ترتيب المعادلة، من ذلك:

و (س) = الفأس ² + ب س + ج

الى هذا:

و (خ) = أ (XH) ² + ك

أين:

ح = -b / 2A
ك = و ( ح )

وبعبارة أخرى، حساب ح (= -b / 2A)، ثم تجد ك عن طريق حساب المعادلة كلها ل س = ح

أولا وقبل كل شيء ... لماذا؟

حسنا، والشيء الرائع عن هذا النموذج الجديد هو أن ساعة و ك تبين لنا أدنى جدا (أو أعلى جدا) نقطة، دعت قمة الرأس : وكذلك منحنى غير متناظرة (صورة طبق الأصل) حول محور يمر من خلال س = ح ، مما يجعل  من السهل على الرسم البياني

وبالتالي ...

• ح يبين لنا مدى اليسار (أو اليمين) وقد تحول منحنى من س = 0
• ك يبين لنا مدى تصل (أو لأسفل) وقد تحول منحنى من ص = 0

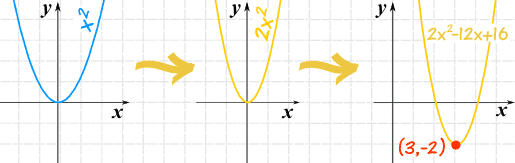
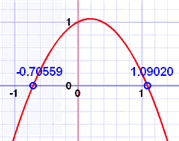
دعونا نرى مثالا على كيفية القيام بذلك:

مثال: قطعة و (س) = 2X ² - 12X + 16

أولا، دعونا يدون:

• و= 2،
• ب = -12، و
• ج = 16

والآن، ما الذي نعرفه؟

• وهو إيجابي، لذلك هو "صعودا" الرسم البياني ( "U" على شكل)
• وهو 2، لذلك فمن قليلا "سحق" مقارنة س ² الرسم البياني

بعد ذلك، دعونا حساب ح:

ح = -b / 2A = - (- 12) / (2X2) = 3

وبعد ذلك يمكننا حساب ك (باستخدام ح = 3):

ك = و ( 3 ) = 2 (3) ² - 12 · 3 + 16 = 18-36 + 16 = -2

وحتى الآن يمكننا رسم بياني (مع الفهم الحقيقي!):

ونحن نعلم أيضا: على قمة الرأس هي (3، -2)، و محور هو س = 3

من الرسم البياني للمعادلة

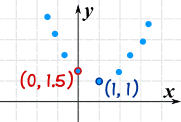
ما إذا كان لدينا الرسم البياني، وترغب في العثور على المعادلة؟

على سبيل المثال: كنت قد خططت فقط بعض البيانات مثيرة للاهتمام، ويبدو التربيعية:

مجرد معرفة هاتين النقطتين يمكننا التوصل إلى معادلة.

أولا، ونحن نعلم ساعة و ك (في الرأس):

(ح، ك) = (1،1)

لذلك دعونا نضع ذلك في هذا النوع من المعادلة:

و (خ) = أ (XH) ² + ك

و (خ) = أ (س-1) ² + 1

ثم نحسب "أ":

نحن نعرف (0، 1.5) وذلك:		و (0) = 1.5
ونحن نعرف وظيفة (باستثناء):		و (0) = أ (0-1) 2 + 1 = 1.5
تبسيط:		و (0) = أ + 1 = 1.5
		و= 0.5

وحتى هنا هو معادلة من الدرجة الثانية مما أدى:

و (س) = 0.5 (خ-1) ² + 1

ملاحظة: هذا قد لا يكون الصحيحة المعادلة للبيانات، ولكن هذا نموذج جيد وأفضل ما يمكن أن تصل.