المعادلات التربيعية

مثال على معادلة من الدرجة الثانية :

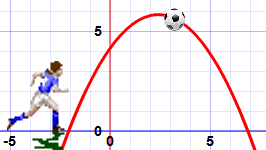
المعادلات التربيعية جعل منحنيات جميلة، مثل هذا واحد:

اسم

اسم الدرجة الثانية يأتي من "رباعية" يعني مربع، لأن المتغير يحصل تربيع (مثل س ² ).

ويطلق عليه أيضا "معادلة درجة 2" (بسبب "2" على س )

النموذج القياسي

في نموذج قياسي من الدرجة الثانية معادلة يبدو مثل هذا:

و ، ب و ج ومن المعروف القيم. و لا يمكن أن يكون 0. " س " هو متغير أو غير معروف (نحن لا نعرف حتى الآن).

وفيما يلي بعض الأمثلة أكثر:

2X 2 + 5X + 3 = 0		في هذا واحد ل= 2 ، ب = 5 و ج = 3
س 2 - 3X = 0		هذا واحد هو أكثر قليلا صعبة: أين هو من ؟ حسنا ل= 1 ، ونحن عادة لا يكتب "1X 2 " ب = -3 وأين هو ج ؟ حسنا ج = 0 ، بحيث لا يظهر.
5X - 3 = 0		وجه الفتاة! هذا هو واحد لا معادلة من الدرجة الثانية: أنه يفتقد س 2  (وبعبارة أخرى ل= 0 ، مما يعني أنه لا يمكن أن يكون من الدرجة الثانية)

مخفي التربيعية المعادلات!

وبالتالي فإن "النموذج القياسي" من الدرجة الثانية المعادلة

الفأس ² + ب س + ج = 0

لكن في بعض الأحيان معادلة من الدرجة الثانية لا تبدو مثل ذلك! فمثلا:

متنكر	→	في نموذج قياسي	أ، ب، ج
س 2 = 3X - 1	نقل كافة الشروط على الجانب الأيسر	س 2 - 3X + 1 = 0	و= 1، ب = -3، ج = 1
2 (ث 2 - 2W) = 5	توسيع (التراجع عن الأقواس )، ونقل 5 إلى اليسار	2W 2 - 4W - 5 = 0	و= 2، ب = -4، ج = -5
ض (ض-1) = 3	التوسع، ونقل 3 إلى اليسار	ض 2 - ض - 3 = 0	و= 1، ب = -1، ج = -3

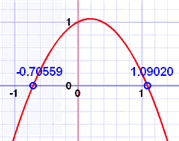وقد للعب معها لعب مع " الدرجة الثانية معادلة إكسبلورر " حتى تستطيع أن ترى: الرسم البياني يجعل، و الحلول (وتسمى "الجذور").

كيفية حلها؟

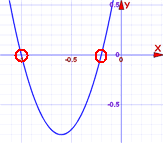
و" الحلول " إلى الدرجة الثانية المعادلة هي حيث أنها تساوي الصفر .

عادة ما تكون هناك 2 الحلول (كما هو موضح في الرسم البياني أعلاه).

فهي تسمى أيضا " جذور "، أو في بعض الأحيان " الأصفار "

هناك 3 طرق لإيجاد الحلول:

1. يمكننا عامل في الدرجة الثانية (تجد أن تتضاعف لجعل الدرجة الثانية معادلة)

2. يمكننا أن أكمل ساحة ، أو

3. يمكننا استخدام الخاصة الصيغة التربيعية :

مجرد سد العجز في قيم أ، ب، ج، والقيام الحسابات.

وسنتطرق في هذا الأسلوب في مزيد من التفاصيل الآن.

حول الصيغة التربيعية

بالإضافة إلى / ناقص

أولا وقبل كل ما هو زائد / ناقص شيء يشبه ± ؟

و ± يعني أن هناك إجابتين: هنا هو السبب في أننا يمكن الحصول على إجابتين:

لكن في بعض الأحيان لم نحصل على إجابتين حقيقية، و "التمايز" يبين لماذا ...

التمايز

هل ترى ب ² - 4AC في الصيغة أعلاه؟ ومن دعا التمايز ، لأنها يمكن أن "التمييز" بين الأنواع الممكنة من الجواب:

عندما ب ² - 4AC إيجابية، ونحن الحصول على اثنين من ريال مدريد الحلول
عندما يكون الصفر نحصل على حل حقيقي واحدة فقط (سواء الإجابات هي نفسها)
عندما يكون سلبيا علينا الحصول على اثنين من مجمع حلول

الحلول المعقدة؟ دعونا نتحدث عنهم بعد أن نرى كيفية استخدام الصيغة.

باستخدام الصيغة التربيعية

وضعت للتو قيم أ، ب، ج في الصيغة التربيعية، والقيام الحسابات.

مثال: حل 5x² + 6X + 1 = 0

معاملات هي:		و= 5، ب = 6، ج = 1
الصيغة التربيعية:		س = -b ± √ (ب2- 4AC)2A
ضع في أ، ج ب و:		س = -6 ± √ (62- 4 × 5 × 1)2 × 5
حل :		س = -6 ± √ (36- 20)10
		س = -6 ± √ (16)10
		س = -6 ± 410
		س = -0.2 أو -1

الجواب: س = -0.2 أو س = -1 ونحن نراهم على هذا الرسم البياني.

تحقق -0.2 :	5 × ( -0.2 ) ² + 6 × ( -0.2 ) + 1 = 5 × (0.04) + 6 × (-0.2) + 1 = 0،2-1،2 + 1 = 0
تحقق -1 :	5 × ( -1 ) ² + 6 × ( -1 ) + 1 = 5 × (1) + 6 × (-1) + 1 = 5-6 + 1 = 0

تذكر الفورمولا

واقترح القارئ نوع الغناء إلى "البوب ​​يذهب لابن عرس":

♫	"س يساوي ناقص ب		♫	"جميع في جميع أنحاء بوش التوت
	زائد أو ناقص الجذر التربيعي			مطاردة القرد ابن عرس
	من ب-تربيع ناقص أربعة ميلان			فكر القرد 'التوا في كل متعة
	ALL أكثر من ل"			البوب! وغني عن ابن عرس "

محاولة الغناء عليه عدة مرات، وسوف تتعثر في رأسك!

أو يمكنك تذكر هذه القصة:

س = -b ± √ (ب²- 4AC)2A

"صبي السلبي كان يفكر بنعم أو لا عن الذهاب الى الحزب،
في الحزب تحدث لصبي مربع ولكن ليس إلى 4 فراخ رهيبة.
كان كل شيء في أكثر من 02:00. "

حلول معقدة؟

عندما التمايز (قيمة ب ² - 4AC ) هو سلبي نحصل على مجمع حلول ... ماذا يعني ذلك؟

وهذا يعني ردنا سوف تشمل أرقام خيالية . نجاح باهر

مثال: حل 5x² + 2X + 1 = 0

معاملات هي :		و= 5، ب = 2، ج = 1
لاحظ أن التمايز هو سلبي:		ب 2 - 4AC = 2 2 - 4 × 5 × 1 = -16
استخدام الصيغة التربيعية:		س = -2 ± √ (-16)10
الجذر التربيعي -16 هو 4 ط ( ط هو √-1، وقراءة أرقام وهمية لمعرفة المزيد)
وبالتالي:		س = -2 ± 4ط10

الجواب: س = -0.2 ± 0.4 ط الرسم البياني لا يعبر المحور س. وهذا هو السبب في أننا انتهى مع الأعداد المركبة.

في بعض الطرق أنه من الأسهل: نحن لا تحتاج إلى مزيد من حساب، مجرد ترك الأمر كما -0.2 ± 0.4 ط .

ملخص

معادلة من الدرجة الثانية في نموذج قياسي: الفأس ² + ب س + ج = 0
المعادلات من الدرجة الثانية يمكن الحسبان
الفورمولا الدرجة الثانية: س = -b ± √ (ب²- 4AC)2A
عندما التمايز ( ب ² -4ac ) هي:
• إيجابية، وهناك 2 حلول حقيقية
• صفر، لا يوجد حل واحد حقيقي
• سلبية، وهناك 2 الحلول المعقدة