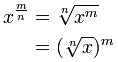قوانيين الجذور في الرياضيات

الأس عدد يقول كم مرة لاستخدام رقم في الضرب. في هذا المثال: 8 2 = 8 × 8 = 64 وبعبارة: 8 2 يمكن أن يسمى "8 إلى القوة الثانية"، "8 إلى قوة 2" أو ببساطة "8 مربع"

مثال آخر: 5 ³ = 5 × 5 × 5 = 125

الدعاة كسور

ولكن ماذا لو كان الأس هو جزء بسيط؟

داعية من 1 / 2 هو في الواقع الجذر التربيعي داعية من 1 / 3 هو مكعب الجذر داعية من 1 / 4 هو الجذر 4TH وما إلى ذلك وهلم جرا!

لماذا ا؟

دعونا نرى ماذا في مثال.

أولا، قوانين الدعاة تقول لنا كيفية التعامل مع الدعاة عندما تتكاثر:

على سبيل المثال: س ² س ² = (س س) (س س) = س س س س= س ⁴

مما يدل على ان س ² س ² = س ^{(2 + 2)} = س ⁴

لذلك دعونا نحاول أن مع الأسس الكسرية:

مثلا: ما هو 9 ^½ × 9 ^½ ؟

9 ^½ × 9 ^½ = 9 ^{(½ + ½)} = 9 ⁽¹⁾ = 9

حتى 9 ^½ الأوقات نفسها تعطي 9.

ماذا نسمي عددا أنه عندما مضروبا في نفسه، ويعطي رقم آخر؟ و الجذر التربيعي !

نرى:

9√ ×9 √ = 9

و:

9 ^½ × 9 ^½ = 9

حتى 9 ^½ هو نفس 9√

محاولة كسر آخر

دعونا نحاول ذلك مرة أخرى، ولكن مع الأس من ربع (1/4):

مثال: 16 ^¼

16 ^¼ × 16 ^¼ × 16 ^¼ × 16 ^¼ = 16 ^{(¼ ¼ + + + ¼ ¼)} = 16 ⁽¹⁾ = 16

حتى 16 ^¼ ، عندما تستخدم 4 مرات في الضرب يعطي 16،

وحتى 16 ^¼ هو جذر 4th من 16

قاعدة عامة

لأنها عملت ½ ، لأنها عملت مع ¼ ، في الواقع يعمل عموما:

س ^{1 / ن} = و N- الجذر عشر من س

حتى نتمكن من التوصل إلى هذا:

A الأس كسور مثل 1 / ن وسيلة ل أخذ الجذر ن عشر :

على سبيل المثال: ما هو 27 ^1/3 ؟

الجواب: 27 ^1/3 = 27 = 3

ماذا عن الكسور أكثر تعقيدا؟

ماذا عن الأس كسور مثل 4 ^3/2 ؟

هذا ما يقول حقا للقيام مكعب (3)، و الجذر التربيعي (1/2)، في أي أمر.

دعني أشرح.

A جزء (مثل م / ن ) يمكن تقسيمها إلى قسمين:

• جزء رقم صحيح ( م )، و
• جزء ( 1 / ن ) جزء

ذلك، لأن م / ن = م × (1 / ن) يمكننا أن نفعل ذلك:

الأمر لا يهم، لذلك يعمل أيضا ل م / ن = (1 / ن) × م :

ونحصل على هذا:

A الأس كسور مثل م / ن يعني:   هل السلطة متر عشر ، ثم أخذ الجذر ن عشر أو خذ الجذر ن عشر ومن ثم القيام السلطة متر التاسع

بعض الأمثلة:

على سبيل المثال: ما هو 4 ^3/2 ؟

4 ^3/2 = 4 ^{3 × (1/2)} = (4 ³ ) √ =(4 × 4 × 4) √  = (64)√  = 8

أو

4 ^3/2 = 4 ^{(1/2) × 3} = (4√) ³ = (2) ³ = 8

وفي كلتا الحالتين يحصل على نفس النتيجة.

 الآن ... اللعب مع الرسم البياني!

انظر كيف بسلاسة يغير منحنى عندما تلعب مع الكسور في هذه الرسوم المتحركة، وهذا يظهر لك أن هذه الفكرة من الأسس الكسرية يناسب معا بشكل  جيد:

الرسم البياني ل= ص س ^{(م / ن)}

م = 1

ن = 2

ص = س ^(1/2)
   = س ^0.5

© 2015 MathsIsFun.com ضد 0.81

أشياء لمحاولة:

• بدء مع م = 1 و n = 1، ثم زيادة ن ببطء بحيث يمكنك ان ترى 1/2، 1/3 و 1/4
• ثم حاول م = 2 والانزلاق ن صعودا وهبوطا لرؤية الكسور مثل 2/3 الخ
• الآن في محاولة لجعل الأس -1
• وأخيرا حاول زيادة م، ثم خفض ن، ثم خفض م، ثم زيادة ن: منحنى يجب أن يرحل وحولها