قوانين القوى والاسس

يقول عدد الأس كم مرة لإستخدام رقم في الضرب. في هذا المثال: 8 2 = 8 × 8 = 64 وبعبارة: 8 2 يمكن أن يسمى "8 إلى القوة الثانية"، "8 إلى قوة 2" أو ببساطة "8 مربع"

انها محاولة لنفسك:

3 ⁴ = 3 × 3 × 3 × 3 = 81

© 2015 v0.81 MathsIsFun.com

لذلك فإن الأس يخلصنا الكتابة من الكثير من الضرب!

على سبيل المثال: ل ⁷

و ⁷ = ل × على × ل × على × ل × على × ل = AAAAAAA

لاحظ كيف كتبنا الحروف معا ليعني مضاعفة؟ وسوف نفعل ذلك الكثير هنا.

على سبيل المثال: س ⁶ = XXXXXX

مفتاح لقوانين

كتابة جميع الرسائل أسفل هو المفتاح لفهم القوانين

على سبيل المثال: س ² س ³ = (س س) (س س س) =   س ⁵

يدل على ان مما س ² س ³ = س ⁵ ، ولكن أكثر عن ذلك لاحقا!

لذلك، عندما تكون في شك، فقط تذكر أن تكتب جميع الحروف (ما يصل إلى يحكي داعية لك) ونرى ما اذا كان يمكنك أن تفهمها.

كل شيئ ترغب بمعرفته ...

"قوانين الدعاة" (وتسمى أيضا "قواعد الدعاة") من تأتي ثلاثة أفكار :

	الأس يقول عدد المرات لإستخدام رقم في الضرب .
	A الأس السلبي يعني الانقسام ، لأن عكس بضرب وتقسيم
	A الأس كسور مثل 1 / ن وسيلة ل أخذ جذر عدد :

إذا فهمت هذه، فإنك تفهم الأسس!

وجميع القوانين أدناه على أساس تلك الأفكار.

قوانين الدعاة

وفيما يلي القوانين (تفسيرات تابع):

القانون	مثال
س 1 = س	6 1 = 6
س 0 = 1	7 0 = 1
س -1 = 1 / س	4 -1 = 1/4
س م س ن = س م + ن	س 2 س 3 = س 2 + 3 = س 5
س م / خ ن = س م ن	س 6 / س 2 = س 2/6 = س 4
(خ م ) ن = س مليون	(س 2 ) 3 = س 2 × 3 = س 6
(س ص) ن = س ن ص ن	(س ص) 3 = س 3 ص 3
(س / ص) ن = س ن / ص ن	(س / ص) 2 = س 2 / ص 2
س -n = 1 / س ن	س -3 = 1 / س 3
والقانون حول كسور الدعاة:

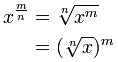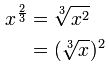قوانين شرح

القوانين الثلاثة الأولى أعلاه ( س ¹ = س ، س ⁰ = 1 و س ^-1 = 1 / س ) ليست سوى جزء من تسلسل الطبيعي من الدعاة. الق نظرة على هذا:

مثال: القوى من 5
	.. الخ ..
5 2	1 × 5 × 5	25
5 1	1 × 5	5
5 0	1	1
5 -1	1 ÷ 5	0.2
5 -2	1 ÷ 5 ÷ 5	0.04
	.. الخ ..

انظروا إلى هذا الجدول لفترة من الوقت ... لاحظت أن الأسس الإيجابية صفر أو سلبية هي في الواقع جزء من النمط نفسه، أي 5 مرات أكبر (أو 5 مرات أصغر) اعتمادا على ما إذا كان الأس يحصل على أكبر (أو أصغر).

آلذي س القانون ^م س ^ن = س ^{م + ن}

مع س ^م س ^ن ، كم مرة أننا لا ينتهي بضرب "س"؟ الجواب: الأولى "م" مرات، ثم من جانب آخر "ن" مرات، ليصبح المجموع "م + ن"  مرات.

على سبيل المثال: س ² س ³ = (س س) (س س س) =  س ⁵

لذلك، س ² س ³ = س ^{(2 + 3)} = س ⁵

على سبيل المثال: س ⁴ / س ² = (س س س س) / (س س) = س س = س ²

لذلك، س ⁴ / س ² = س ^(2/4) = س ²

(آن تذكر س / س = 1، في كل مرة وذلك تشاهد س "فوق خط" واحد "تحت خط" يمكنك منعها من الصدور.)

هذا القانون ايضآ يمكن تظهر لك لماذا س ⁰ = 1 :

على سبيل المثال: س ² / س ² = س ^2/2 = س ⁰ = 1

 

على سبيل المثال: x ³ ) ⁴ = (XXX) ⁴ = (XXX) (XXX) (XXX) (XXX)  XXXXXXXXXXXX = x ¹²

حتى (س ³ ) ⁴ = س ^{3 × 4} = س ¹²

القانون الذي (س ص) ^ن = س ^ن ص ^ن

لاظهار كيف يعمل هذا واحد، مجرد التفكير في إعادة ترتيب كل ليالي "س" والصورة "ص" كما في هذا المثال:

على سبيل المثال: (س ص) ³ = (س ص) (س ص) (س ص) = = = xyxyxy xxxyyy (XXX) (ص ص ص) = س ³ ص ³

القانون الذي (س / ص) ^ن = س ^ن / ص ^ن

على غرار المثال السابق، مجرد إعادة ترتيب ليالي "س" والصورة "ص"

على سبيل المثال: (س / ص) ³ = (س / ص) (س / ص) (س / ص) = (XXX) / (ص ص ص) = س ³ / ص ³

القانون الذي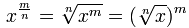 

OK، هذا واحد هو قليلا أكثر تعقيدا!

عليك قراءة أقترح الدعاة كسور أولا، أو أن هذا قد لا يكون له معنى.

على أي حال، فإن الفكرة المهمة هي أن:

س ^{1 / ن} = و N- الجذر عشر من س

وهكذا الأس كسور مثل 4 ^3/2 يقول حقا للقيام مكعب (3)، و الجذر التربيعي (1/2)، في أي أمر.

تذكر من الكسور فقط آلتي م / ن = م × (1 / ن) :

مثال: 

الأمر لا يهم، يعمل ايضآ ل لذلك م / ن = (1 / ن) × م :

مثال: 

وهذا هو عليه!

إذا كنت تجد صعوبة في تذكر كل هذه القواعد، ثم تذكر هذا:

العمل بها عند يمكنك وفهم
الأفكار الثلاثة بالقرب من أعلى هذة الصفحة

أوه، أكثر شيء واحد ... ما إذا كان س = 0؟

الأس الإيجابي (ن> 0)		0 ن = 0
الأس السلبي (ن <0)		غير محدد! (لان قسمة 0 غير معرف)
الأس = 0		يممم ... انظر أدناه!

في حالة غريبة من 0 ⁰

هناك نوعان من حجج مختلفة عن القيمة الصحيحة من 0 ⁰ .

0 ⁰ يمكن أن يكون 1، أو ربما 0، وحتى بعض الناس يقولون انها حقا "غير محدد":

	س 0 = 1، لذلك ...	0 0 = 1
	0 ن = 0، لذلك ...	0 0 = 0
	في حالة الشك ...	0 0 = "غير محدد"