استحدام الرياضيات في التشفير وحماية البنوك (الاعداد الاولية )
والخوف السرية
نحن دائما يقال للحفاظ على البيانات لدينا آمنة، فلماذا أي شخص أريد أن حظر التشفير؟
كان واحدا من أهم تطبيقات الرياضيات في السنوات ال 100 الماضية مما لا شك فيه الأعمال المتصلة التشفير وكسر الشفرة. في نهاية فريق الحرب العالمية الثانية آلان تورينج في حديقة بلتشلي ساهموا في القضاء قانون لغز وساعد تقصير الحرب بما يقدر بنحو عامين، مع عملهم مما يؤدي إلى تطوير أجهزة الكمبيوتر الأولى.
وفي الآونة الأخيرة مع اختراع شبكة الإنترنت، والتشفير يعني أن نتمكن من التواصل بشكل آمن. بدون تشفير أي شخص سيكون قادرا على السهل سرقة بياناتك والتسوق عبر الانترنت فقط لن يكون ممكنا.
في الواقع معظم وقتك على الانترنت ستصبح غير آمن جدا وصعبة. عند نقل تفاصيل حسابك المصرفي عبر الإنترنت يتم الاحتفاظ بها سرا من قبل ما يسمى "الترميز بالمفتاح العمومي. (إذا كنت ترغب في قراءة تفسير رياضي لتشفير المفتاح العام نلقي نظرة على هذه Nrich المادة تستهدف طلاب المستوى A.)
في قلب التشفير بالمفتاح العمومي هو تكاثر الأعداد الأولية. فمن السهل جدا لضرب رقمين معا (على سبيل المثال بضرب 83 مع 71 من السهل). ولكن إذا كنت نظرا لعدد 5893 لكان قد اتخذ لك بعض الوقت لfactorise ذلك والعمل إلى أن 5893. من أجل فك تشفير الرسالة التي تم ترميزها باستخدام الترميز بالمفتاح العمومي تحتاج إلى أن تكون قادرة على factorise ل نظرا عدد بسرعة. إذا كنت تستطيع factorise الأرقام ثم يمكنك كسر التشفير. عندما الأرقام المستخدمة هي أكبر من ذلك بكثير هو أصعب بكثير لfactorise لهم في كمية معقولة من الزمن. في الواقع صعوبة أرقام factorising يعني أنه رياضيا صعبة للغاية على فك الرسائل التي تم تشفيرها باستخدام هذا الأسلوب.
في الماضي كانت هناك وسائل أخرى للتشفير التي كان يعتقد أنها غير قابلة للكسر، لذلك ما هو هناك لوقف شخص ما اختراع خوارزمية المدهشة التي factorises أعداد كبيرة بسرعة كبيرة جدا؟ والسبب هو أن factorising أرقام هو نوع من المشاكل التي تعتقد الرياضيات صعب في الأساس، وهذا يعني أنه من غير المحتمل أن أعدادا كبيرة في أي وقت أن factorised سريع بما فيه الكفاية للرسائل ليتم فك شفرة بكفاءة. (على الرغم من أن علماء الرياضيات لها لا يزال لإثبات هذا على وجه اليقين!)
هل كنت تعلم؟
شبه أولي هو الرقم الذي هو عددين أوليين تضاعفت معا. على سبيل المثال 35 هو شبه أوليه becase 35 = 7 X 5. وفي عام 1991 نشرت RSA مختبرات قائمة عدد نصف أولي، وعرضت جوائز نقدية لعواملها الخاصة بهم. ما زالت لم يكن كلها تم factorised الأرقام، حتى يومنا هذا - تظهر مدى صعوبة عدد نصف أولي factorising هو. وكان أكبر عدد للأن factorised في هذا التحدي 768 أرقام طويلة واستغرق عامين وما يعادل 2000 سنة من قوة الحوسبة!
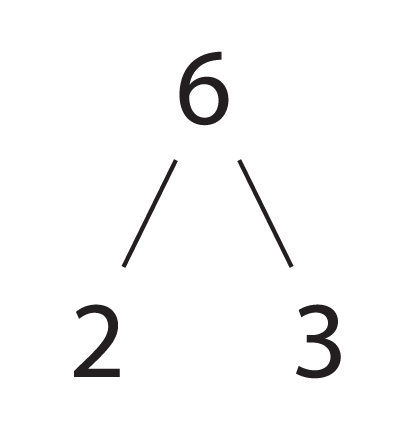
شبه أولي هو الرقم الذي هو عددين أوليين تضاعفت معا. على سبيل المثال 35 هو شبه أوليه becase 35 = 7 X 5. وفي عام 1991 نشرت RSA مختبرات قائمة عدد نصف أولي، وعرضت جوائز نقدية لعواملها الخاصة بهم. ما زالت لم يكن كلها تم factorised الأرقام، حتى يومنا هذا - تظهر مدى صعوبة عدد نصف أولي factorising هو. وكان أكبر عدد للأن factorised في هذا التحدي 768 أرقام طويلة واستغرق عامين وما يعادل 2000 سنة من قوة الحوسبة!

ستة مثال صغير من شبه أوليه.
لذلك نحن في مرحلة في تاريخ البشرية حيث أننا قد اخترع طرق التشفير التي أجدادنا يمكن أن يحلم فقط. فلماذا الحكومات الحصول على أكثر قلقا حول تشفير إذا كان من المفيد جدا، والآن قوي جدا؟
حتى الآن تحدثنا فقط عن فوائد التشفير وكيف يمكننا الحفاظ الرسائل وأموالنا في مأمن من المجرمين. الجانب الثاني هو أن التشفير يمكن أيضا الاستفادة الإرهابيين والمجرمين الذين يريدون التواصل في القطاع الخاص، ومنع وكالات إنفاذ القانون من اعتراض رسائلهم.
حتى الآن تحدثنا فقط عن فوائد التشفير وكيف يمكننا الحفاظ الرسائل وأموالنا في مأمن من المجرمين. الجانب الثاني هو أن التشفير يمكن أيضا الاستفادة الإرهابيين والمجرمين الذين يريدون التواصل في القطاع الخاص، ومنع وكالات إنفاذ القانون من اعتراض رسائلهم.
والسبب أن التشفير هو موضوع ساخن مرة أخرى هو أن بعض خدمات الرسائل مثل واتس اب نفذت ما يعرف ب "وضع حد لتشفير نهاية". في الماضي عندما كنت أرسلت رسالة زيارتها بمزود الخدمة المفتاح لفتح رسائلك.
الفرق مع خدمات مثل واتس اب هو أن رسالتك فك مرة واحدة فقط كان على هاتف الشخص الذي تتصل به. بعبارات بسيطة وهذا يعني أنه حتى لو أراد واتس اب HQ لقراءة رسائلك ثم انهم لا يستطيعون.
هذا هو عندما يصبح مخيفا للحكومات التي فجأة لا يمكن الوصول إلى الاتصالات من الناس الذين يشتبه إرهابيين أو مجرمين. ولكن هناك بعض الطرق المعقدة الأخرى على اعتراض الرسائل التي تستخدم اقصاه الى اقصاه التشفير.
على سبيل المثال يمكن للمستخدم أن تخضع إلى ما يعرف بأنه هجوم رجل في متوسطي عندما يقوم شخص ينتحل جهاز الشخص الذي تتصل به. ويمكن أيضا أن يكون اخترق الهاتف والرسائل قراءة مرة واحدة هم على الجهاز الفعلي وليس عندما تكون في العبور. لدينا الآن معضلة صعبة - حظر أو التشفير الحد الذي قد يؤدي إلى المجرمين الوصول إلى الاتصالات الشعوب أو السماح بهذا النوع القوي من التشفير وتجعل من السهل للمجرمين للتواصل سرا.
المسألة برمتها من مقدار الحكومة يجب أن تكون قادرا على الوصول إلى البيانات الناس هي قضية سياسية واسعة النطاق وهي واحدة من الأماكن التي تجتمع الرياضيات السياسة. مهما كانت وجهة نظركم على حق الناس في الخصوصية، فمن المؤكد أن الرياضيات التشفير قد تغير وجه العالم الحديث على حد سواء للأفضل، وربما أيضا للأسوأ.
المسألة برمتها من مقدار الحكومة يجب أن تكون قادرا على الوصول إلى البيانات الناس هي قضية سياسية واسعة النطاق وهي واحدة من الأماكن التي تجتمع الرياضيات السياسة. مهما كانت وجهة نظركم على حق الناس في الخصوصية، فمن المؤكد أن الرياضيات التشفير قد تغير وجه العالم الحديث على حد سواء للأفضل، وربما أيضا للأسوأ.
إذا كنت مهتما في مهنة في مجال التشفير ثم هناك عدد من الأماكن التي يمكن أن تعمل بما في ذلك جامعة أو شركة خاصة أو في GCHQ (مقر الاتصالات الحكومية). يجب أن تأخذ درجة مع محتوى الرياضية عالية مثل الرياضيات، والإحصاء، الفيزياء أو علوم الكمبيوتر. في العالم الحديث هناك سيكون الطلب المتزايد على ذكية، والناس الموهوبين رياضيا الذين يمكن أن نفهم والعمل مع التكنولوجيا.
إذا كنت مهتما في مسيرته في عالم رياضيات في GCHQ ثم نلقي نظرة على على الموقع .
إذا كنت مهتما في مسيرته في عالم رياضيات في GCHQ ثم نلقي نظرة على على الموقع .
المقال الذي هيزل لويس
الرئيسية الصورة الائتمان: يوري Samollov / فليكر بواسطة CC
الرئيسية الصورة الائتمان: يوري Samollov / فليكر بواسطة CC
استحدام الرياضيات في التشفير وحماية البنوك (الاعداد الاولية )
![استحدام الرياضيات في التشفير وحماية البنوك (الاعداد الاولية )]() Reviewed by . blogmathappily
on
4:29 م
Rating:
Reviewed by . blogmathappily
on
4:29 م
Rating:


