Evolution of numbers تطور الأعداد

تطور الأعداد 

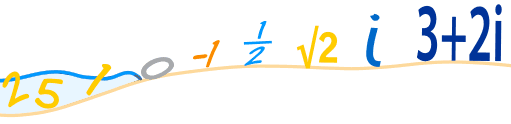
أريد أن يأخذك في مغامرة ...

... مغامرة من خلال عالم الأرقام.

دعونا نبدأ في البداية:

س: ما هو أبسط فكرة العدد؟

A: شيء لل إحصاء مع!

أرقام العد

يمكننا استخدام الأرقام ل العد : 1، 2، 3، 4، الخ

تم البشر يستخدمون أرقام العد مع لآلاف السنين. بل هو شيء طبيعي جدا أن تفعل.

• هل يمكن أن يكون " 3 أصدقاء"،
• حقل يمكن أن يكون " 6 أبقار"
• وما إلى ذلك وهلم جرا.

اذا لدينا:

عد الأرقام: {1، 2، 3، ...}

و "أرقام عد" راض الناس لفترة طويلة.

صفر

فكرة الصفر ، على الرغم من الطبيعي لنا الآن، لم يكن الطبيعية للبشر في وقت مبكر ... إذا كان هناك أي شيء لحساب، كيف يمكنك الاعتماد عليه؟

على سبيل المثال: يمكنك الاعتماد الكلاب، ولكن لا يمكن الاعتماد مساحة فارغة:

كلبان		صفر الكلاب؟ صفر القطط؟

التصحيح فارغة من العشب هو مجرد التصحيح فارغة من العشب!

نائب

ولكن منذ حوالي 3000 سنة الناس بحاجة إلى معرفة الفرق بين الأرقام كما 4 و 40. دون الصفر فإنها تبدو هي نفسها!

لذا استخدموا "نائبا"، مسافة أو رمز خاص، لإظهار "لا توجد أرقام هنا"

5 2	حتى "5 2" تعني "502" (5 المئات، ليس للعشرات، و 2 وحدة)

وكانت الفكرة من الصفر بدأت، ولكن لم يكن لسنوات أخرى ألف أو حتى أن الناس بدأت التفكير في الأمر باعتباره الفعلي عدد .

ولكن الآن يمكن أن نفكر

"كان لي 3 البرتقال، ثم أكلت 3 البرتقال، والآن لدي الصفر البرتقال ...!"

أرقام كاملة

لذا، دعونا إضافة صفر إلى أرقام العد إلى جعل مجموعة جديدة من الأرقام.

ولكن نحن بحاجة إلى اسم جديد، وهذا الاسم هو "الأعداد الصحيحة":

أرقام كاملة : {0، 1، 2، 3، ...}

أرقام الطبيعية

قد تسمع أيضا مصطلح " أرقام طبيعية " ... الذي يمكن أن يعني:

• "الأرقام عد": {1، 2، 3، ...}
• أو أن "الأعداد الصحيحة": {0، 1، 2، 3، ...}

اعتمادا على هذا الموضوع. أعتقد أنهم يختلفون حول ما إذا كان الصفر هو "طبيعي" أم لا.

أرقام سلبية

ولكن تاريخ الرياضيات هو كل شيء عن الناس طرح الأسئلة، وتسعى الأجوبة!

أحد الأسئلة جيدة للنطلبه هو

"اذا كان يمكنك الذهاب في اتجاه واحد، يمكنك الذهاب إلى عكس ذلك الطريق؟"

نستطيع أن نعول الأمام: 1، 2، 3، 4، ...

... ولكن ماذا لو نحن نعول الوراء: 3، 2، 1، 0، ... ماذا يحدث بعد ذلك؟

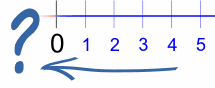الجواب: يمكنك الحصول على الأرقام السالبة:

الآن يمكننا أن نذهب إلى الأمام وإلى الوراء بقدر ما نريد

ولكن كيف يمكن للعدد أن يكون "سلبيا"؟

بمجرد أن يكون أقل من الصفر.

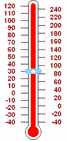وهناك مثال بسيط هو درجة الحرارة . نحدد الصفر درجة مئوية ( 0 درجة مئوية ) ليكون عندما يتجمد الماء ... ولكن اذا حصلنا على  برودة نحتاج درجات الحرارة السلبية. حتى -20 ° C 20 درجة تحت الصفر.

الأبقار السلبية؟

ونظريا يمكن لديك بقرة السلبية!

التفكير في هذا الأمر ... إذا كنت للتو باع اثنين من الثيران ، ولكن لا يمكن إلا أن العثور على واحد لتسليم المالك الجديد ... كنت في الواقع لدينا ناقص ثورا واحدا ... كنت في الديون الثور واحد!

حتى الأرقام السالبة موجودة، ونحن سنحتاج الى مجموعة جديدة من الأرقام لتضمينها ...

الأعداد الصحيحة

إذا كان لنا أن تشمل الأرقام السالبة مع أرقام كاملة، لدينا مجموعة جديدة من الأرقام التي تسمى الأعداد الصحيحة

الأعداد الصحيحة: {...، -3، -2، -1، 0، 1، 2، 3، ...}

وتشمل الأعداد الصحيحة الصفر، أرقام العد، والسلبية للأرقام العد، لتقديم قائمة من الأرقام التي تمتد في كلا الاتجاهين لأجل غير مسمى.

الكسور

إذا كان لديك برتقالة واحدة ويريدون تقاسمها مع شخص ما، تحتاج إلى قطع عليه في النصف. لقد اخترع مجرد نوع جديد من العدد!

كنت أخذت رقم (1)، ومقسوما على عدد آخر (2) من أجل التوصل إلى النصف (1/2)

الشيء نفسه يحدث عندما يكون لدينا أربعة البسكويت (4) وترغب في مشاركتها بين ثلاثة أشخاص (3) ... يحصلون على (4/3) البسكويت لكل منهما.

وهناك نوع جديد من العدد، واسم جديد:

أرقام نسبية

ويسمى أي رقم يمكن كتابة ككسر رقم الرشيد.

لذا، إذا "ع" و "س" هي الأعداد الصحيحة (تذكر تحدثنا عن الأعداد الصحيحة)، ثم ص / ف هو رقم منطقي.

مثال: إذا ص هو 3 و ف هو 2، ثم:

ص / ف = 3/2 = 1.5 هو رقم منطقي

المرة الوحيدة التي لم ينجح هذا هو عندما ف هو صفر، لأن القسمة على الصفر هو غير معروف.

أرقام الرشيد : {ص / ف: p و ف هي الأعداد الصحيحة، ف ليس صفرا}

حتى نصف ( ½ ) هو رقم منطقي.

و 2 هو رقم منطقي أيضا، لأنك يمكن أن يكتب ك 2/1

لذلك، وتشمل أرقام الرشيد:

• جميع الأعداد الصحيحة
• وجميع الكسور .

حتى عدد مثل 13،3168980325 هو عدد العقلاني.

13،3168980325 = 133168980325/10000000000

ويبدو أن تشمل جميع الأرقام الممكنة، أليس كذلك؟

ولكن هناك ما هو أكثر

لم يكن الناس التوقف عن طرح الأسئلة ... وهنا هو واحد التي تسببت في الكثير من الضجة في عهد فيثاغورس:

إذا كنت رسم مربع (من حجم "1")، ما هي المسافة عبر قطري؟

الجواب هو الجذر التربيعي من 2 ، وهو 1،4142135623730950 ... (الخ)

ولكنه ليس عددا مثل 3 أو 5/3، أو أي شيء من هذا القبيل ...

... في الواقع كنت لا يمكن الإجابة على هذا السؤال باستخدام نسبة عددين

الجذر التربيعي ل 2 ≠ ص / ف

... وذلك هو ليس عددا العقلاني (اقرأ المزيد هنا )

نجاح باهر هناك أعداد التي ليست أرقام عقلانية! ماذا نسميها؟

ما هو "غير عقلاني" ...؟ غير منطقي !

أرقام غير منطقية

لذا، فإن الجذر التربيعي ل 2 (√2) هو غير عقلاني عدد. ومن دعا غير منطقي لأنه ليست عقلانية (لا يمكن أن يتم باستخدام نسبة بسيطة من الأعداد الصحيحة). أنه ليس مجنونا أو أي شيء، فقط لا عقلانية.

ونحن نعرف أن هناك العديد من الأرقام أكثر غير عقلانية. بي ( π ) هي واحدة الشهير.

مفيد

حتى أرقام غير منطقية مفيدة. كنت في حاجة إليها ل

• إيجاد المسافة القطرية عبر بعض الساحات،
• للعمل على الكثير من الحسابات مع الدوائر (باستخدام π )،
• و اكثر،

ولذا فإننا يجب أن تتضمن حقا لهم.

وهكذا، ونحن نقدم مجموعة جديدة من الأرقام ...

أرقام حقيقية

هذا صحيح، اسم آخر!

وتشمل الأرقام الحقيقية:

• الأرقام عقلانية، و
• أرقام غير منطقية

الأرقام الحقيقية: {س: x هو عقلاني أو عدد غير نسبي}

في الواقع العدد الحقيقي يمكن اعتبار أي نقطة في أي مكان على خط الأعداد:

© 2015 v0.77 MathsIsFun.com

وهذا يدل سوى عدد قليل من المنازل العشرية (انها مجرد كمبيوتر بسيط)
ولكن يمكن أن الأعداد الحقيقية لديها الكثير من الأماكن العشرية !

أي نقطة في أي مكان على خط الأعداد، وهذا هو بالتأكيد أرقام يكفي!

ولكن هناك رقم واحد أكثر التي تحولت إلى أن تكون مفيدة جدا. ومرة أخرى، جاءت من السؤال.

تخيل ...

السؤال هو:

"هناك الجذر التربيعي من ناقص واحد ؟"

وبعبارة أخرى، ما يمكن أن تتضاعف في حد ذاته للحصول على -1 ؟

نفكر في هذا: إذا كنت ضرب أي عدد في حد ذاته لا يمكنك الحصول على نتيجة سلبية:

• 1 × 1 = 1 ،
• وأيضا (-1) × (-1) = 1 (لأن الأوقات السلبية سلبي يعطي إيجابية )

وماذا في ذلك العدد، عندما مضروبا في نفسه، والنتائج في -1 ؟

هذا هو عادة غير ممكن، ولكن ...

"إذا كنت تستطيع تخيل ذلك، ثم يمكنك اللعب معها"

وبالتالي، ...

أرقام خيالية

... دعونا فقط تخيل أن الجذر التربيعي لناقص واحد موجود . حتى أننا يمكن أن تعطيه رمز خاص: الرسالة ط

ويمكننا استخدامها للإجابة على الأسئلة:

على سبيل المثال: ما هو الجذر التربيعي لل-9؟

الجواب: √ (-9) = √ (9 × -1) = √ (9) × √ (-1) = 3 × √ (-1) = 3 ط

OK، والجواب لا يزال ينطوي ط ، لكنه يعطي معقولة و تتماشى الجواب.

و أنا لديها هذا العقار المميز أنه إذا كنت تربيع ذلك ( ط × ط ) تحصل -1 الذي يعود إلى كونه الرقم الحقيقي. في الواقع هذا هو التعريف الصحيح:

عدد وهمي : عدد الذين مربع هو سلبي العدد الحقيقي.

و ط (الجذر التربيعي ل -1) مرات أي عدد حقيقي هو عدد وهمي. لذلك فان هذه كلها أرقام خيالية:

• 3 ط
• -6 ط
• 0.05 ط
• π ط

وهناك أيضا العديد من التطبيقات لأرقام خيالية، على سبيل المثال في مجالات الكهرباء والالكترونيات.

ريال مقابل أرقام خيالية

وضحك أرقام وهمية أصلا في، وهكذا حصلت على اسم "وهمية". وحصلت على الأعداد الحقيقية اسمها إلى تمييزها عن أرقام خيالية.

وبالتالي فإن الأسماء هي مجرد شيء التاريخي. الأرقام الحقيقية ليست "في العالم الحقيقي" (في الواقع، في محاولة لايجاد بالضبط نصف شيء في العالم الحقيقي!) وأرقام وهمية ليست "فقط في الخيال" ... وكلاهما أنواع صالحة ومفيدة أرقام!

في الواقع كثيرا ما تستخدم معا ...

"ماذا لو كنت وضعت الرقم الحقيقي و عدد وهمي معا؟"

ارقام مركبة

نعم، إذا وضعت رقم ريال مدريد وعدد وهمي معا تحصل على نوع جديد من عدد يسمى عدد مجمع وهنا بعض الأمثلة:

• 3 + 2 ط
• 27،2-11،05 ط

الرقم مجمع يحتوي على جزء حقيقي وجزء وهمي، ولكن أي واحد يمكن أن يكون صفرا

ولذلك فإن العدد الحقيقي هو أيضا عدد مجمع (مع الجزء التخيلي من 0):

• 4 هو عدد مجمع (لأنه هو 4 + 0 ط )

وكذلك على رقم وهمي هو أيضا عدد مجمع (مع جزء حقيقي من 0):

• 7 ط هو رقم مجمع (لأنه هو 0 + 7 ط )

حتى تشمل الأعداد المركبة عن الأعداد الحقيقية وجميع أرقام خيالية، وجميع مجموعات منهم.

وهذا كل شيء!

هذا كل أنواع العدد الأكثر أهمية في الرياضيات.

من أرقام العد وصولا إلى الأعداد المركبة.

وهناك أنواع أخرى من الأرقام، لأن الرياضيات هو موضوع واسع، ولكن هذا يجب أن نفعل لك في الوقت الراهن.

ملخص

ها هم مرة أخرى:

نوع من عدد	الوصف سريع
عد الأرقام	{1، 2، 3، ...}
الأعداد الكلية	{0، 1، 2، 3، ...}
الأعداد الصحيحة	{...، -3، -2، -1، 0، 1، 2، 3، ...}
أرقام نسبية	ص / ف: p و ف أعداد صحيحة، ف ليس صفرا
أرقام غير منطقية	لا عقلاني
أرقام حقيقية	Rationals واللا عقلانيون
أرقام خيالية	تربيع منهم يعطي الرقم الحقيقي السلبي
ارقام مركبة	مجموعات من الأعداد الحقيقية والخيالية

نهاية ملاحظات

التاريخ

تاريخ الرياضيات واسع جدا، مع الثقافات المختلفة (الإغريق والرومان والعربية والصينية والهندية والأوروبية) التالية مسارات مختلفة، والعديد من المطالبات ل "فكرنا في لأول مرة!" ، ولكن الترتيب العام لاكتشاف ناقشت هنا يعطي فكرة جيدة عن ذلك.

الأسئلة

وليس من المدهش كم عدد المرات التي يسأل سؤالا، مثل

• "ماذا يحدث إذا نحن نعول الوراء من خلال الصفر" ، أو
• "ما هي المسافة بالضبط عبر قطري للمربع"

أدى أول من الخلاف (وحتى السخرية!)، ولكن في نهاية المطاف إلى تحقيق اختراقات مذهلة في التفاهم.

وأتساءل ما يجري سأل أسئلة مثيرة للاهتمام الآن؟

زيادة لك!

وهنا اثنين من الأسئلة التي يمكن طرحها عند تتعلم شيئا جديدا:

يمكن أن تذهب في الاتجاه الآخر؟

• أرقام إيجابية تؤدي إلى الأرقام السالبة
• الساحات تؤدي الى المربع جذور
• إلخ

هل يمكنني استخدام هذا مع شيء آخر وأنا أعلم؟

• إذا كانت الأرقام، فإنها يمكن أن تضاف كسور، تطرح، وما إلى ذلك؟
• هل يمكنني أخذ الجذر التربيعي لعدد معقدة؟ (هل تستطيع؟)
• إلخ