مثلثات

مثلثات

	مثلث له ثلاثة جوانب وثلاث زوايا
	الزوايا الثلاث دائما إضافة إلى 180 °

متساوي الأضلاع، متساوي الساقين ومختلف الأضلاع

هناك ثلاثة أسماء خاصة بالنظر إلى مثلثات أن أقول كم من الجانبين (أو زوايا) على قدم المساواة.

يمكن أن يكون هناك 3 ، 2 أو أي الجانبين على قدم المساواة / زوايا:

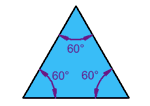	مثلث متساوي الاضلاع ثلاثة أضلاع متساوية ثلاث زوايا متساوية، دائما 60 درجة
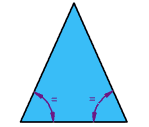	مثلث متساوي الساقين اثنين من الجانبين على قدم المساواة اثنين من زوايا متساوية
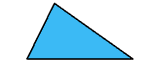	مثلث مختلف الأضلاع لا أضلاع متساوية لا زوايا متساوية

ما هو نوع من زاوية؟

يمكن مثلثات أيضا الأسماء التي اقول لكم ما نوع من زاوية هو في الداخل :

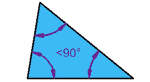	مثلث حاد الزوايا جميع الزوايا أقل من 90 درجة
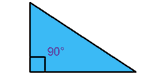	مثلث قائم لديه زاوية قائمة (90 درجة)
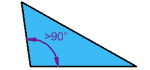	منفرجة المثلث لديه أكثر من زاوية 90 درجة

الجمع بين أسماء

في بعض الأحيان سوف مثلث واثنين من الأسماء، على سبيل المثال: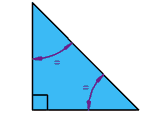

الصحيح متساوي الساقين المثلث لديه زاوية قائمة (90 درجة)، وأيضا اثنين من زوايا متساوية هل يمكنك تخمين ما هي زوايا متساوية؟

العب به ...

محاولة سحب النقاط حولها وجعل مثلثات مختلفة:

قد ترغب أيضا للعب مع المثلث التفاعلية .

محيط

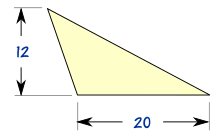
محيط هي المسافة حول حافة المثلث: إضافة للتو الاطراف الثلاثة:

منطقة

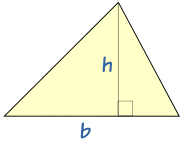
وهذه المنطقة هي نصف الارتفاع مرة قاعدة .

• "ب" هو المسافة على طول قاعدة
• "ح" هو ارتفاع (تقاس بزاوية قائمة على قاعدة)

المساحة = ½ × ب × ح

الصيغة تعمل لجميع مثلثات.

ملاحظة: طريقة أسهل من كتابة الصيغة البوسنة والهرسك / 2

على سبيل المثال: ما هي مساحة هذا المثلث؟

(ملاحظة: 12 هي ارتفاع ، وليس طول الجانب الأيسر)

ارتفاع = ح = 12

قاعدة = ب = 20

المساحة = ½ × ب × ح = ½ × 20 × 12 = 120

القاعدة يمكن أن يكون أي طرف، فقط تأكد من أن يقاس "ارتفاع" في زوايا الحق في "القاعدة" :

(ملاحظة: يمكنك أيضا حساب مساحة من أطوال الأضلاع الثلاثة باستخدام صيغة هيرو ).

لماذا هو منطقة "نصف البوسنة والهرسك"؟

تخيل أنك "الضعف" المثلث (الوجه حولها واحدة من الحواف العلوية) لجعل مثل مربع الشكل (أ متوازي الاضلاع ) والتي يمكن تغييرها إلى بسيطة المستطيل :

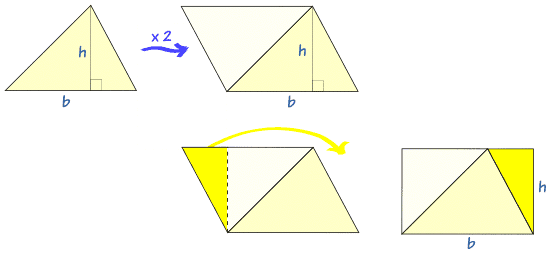
ثم المنطقة كلها البوسنة والهرسك ، والتي هي على حد سواء مثلثات، وذلك فقط واحد هو ½ × البوسنة والهرسك .