الجمال الخفية للجداول الضرب
https://plus.maths.org/content/sites/plus.

ارسل بواسطة ماريان في 7 أبريل 2017
وسوف نضيف صف من 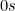 على رأس وعمود
على رأس وعمود 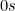 على اليسار. هذا لا يزال يعطي الجدول ثابت - الصف الأول والعمود يحتوي على مضاعفات
على اليسار. هذا لا يزال يعطي الجدول ثابت - الصف الأول والعمود يحتوي على مضاعفات  ، الصف الثاني والعمود يحتوي على مضاعفات
، الصف الثاني والعمود يحتوي على مضاعفات  ، الصف الثالث والعمود يحتوي على مضاعفات
، الصف الثالث والعمود يحتوي على مضاعفات 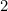 ، وما إلى ذلك - وأنها سوف توفر إطارا لطيفة لأنماط لدينا.
، وما إلى ذلك - وأنها سوف توفر إطارا لطيفة لأنماط لدينا.
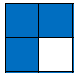
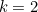 : نحن تعيين اللون الأزرق إلى كل مربع في جدول الضرب الذي هو من مضاعفات الرقم
: نحن تعيين اللون الأزرق إلى كل مربع في جدول الضرب الذي هو من مضاعفات الرقم 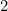 . (عدد
. (عدد 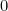 من مضاعفات
من مضاعفات 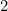 ، لذلك كل
، لذلك كل 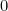 الساحات والأزرق).
الساحات والأزرق).


 الملونة الحمراء، وتلك التي هي مضاعفات
الملونة الحمراء، وتلك التي هي مضاعفات  وبرتقالية اللون (مع البرتقال أخذ الأسبقية على أحمر في حالة من مضاعفات على حد سواء
وبرتقالية اللون (مع البرتقال أخذ الأسبقية على أحمر في حالة من مضاعفات على حد سواء  و
و 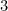 ، أي مضاعفات
، أي مضاعفات 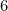 ).
).

الجمال الخفية للجداول الضرب
في هذه المادة ونحن استكشاف بعض التماثلات التي تخفي ضمن جدول الضرب من الأرقام كلها إيجابية.
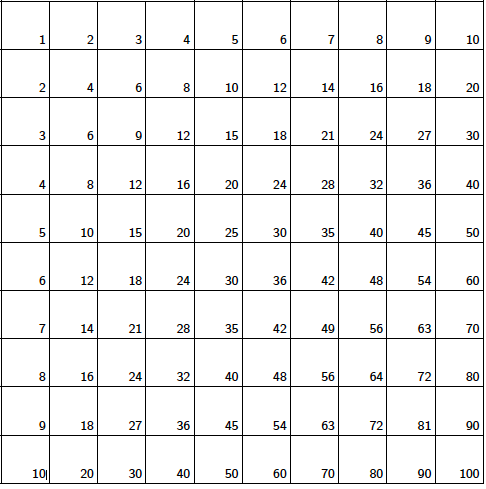
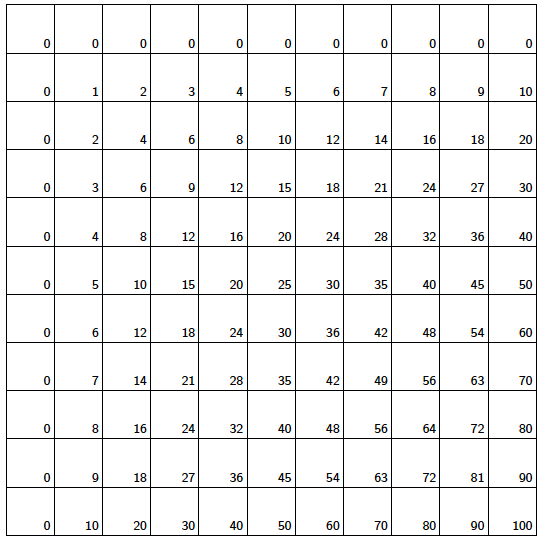
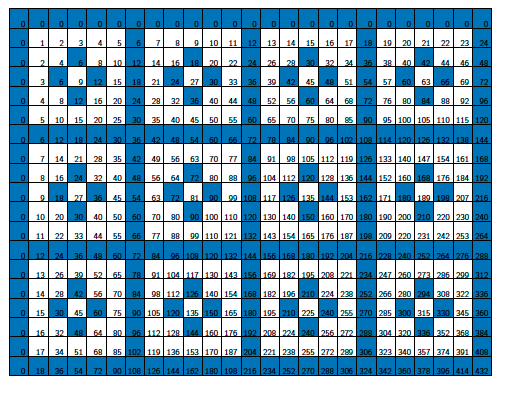
دعونا نبدأ مع جدول الضرب القياسي. ويتضمن الجدول أدناه أعداد 1-10 في الصف الأول والعمود الأول. يحتوي على أي مربع آخر نتاج الرقم الأول في الصف، والرقم الأول في عموده.

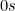 على رأس وعمود
على رأس وعمود 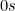 على اليسار. هذا لا يزال يعطي الجدول ثابت - الصف الأول والعمود يحتوي على مضاعفات
على اليسار. هذا لا يزال يعطي الجدول ثابت - الصف الأول والعمود يحتوي على مضاعفات 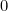 ، الصف الثاني والعمود يحتوي على مضاعفات
، الصف الثاني والعمود يحتوي على مضاعفات  ، الصف الثالث والعمود يحتوي على مضاعفات
، الصف الثالث والعمود يحتوي على مضاعفات 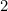 ، وما إلى ذلك - وأنها سوف توفر إطارا لطيفة لأنماط لدينا.
، وما إلى ذلك - وأنها سوف توفر إطارا لطيفة لأنماط لدينا.
في ما يلي، سنقوم لون مربعات جدول الضرب التي تتوافق مع مضاعفات عدد 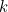 للقيم المختلفة
للقيم المختلفة 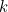 . وسنقوم اكتشاف بعض التماثلات الجميلة.
. وسنقوم اكتشاف بعض التماثلات الجميلة.
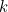 للقيم المختلفة
للقيم المختلفة 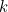 . وسنقوم اكتشاف بعض التماثلات الجميلة.
. وسنقوم اكتشاف بعض التماثلات الجميلة.مضاعفات واحدة
نبدأ مع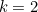 : نحن تعيين اللون الأزرق إلى كل مربع في جدول الضرب الذي هو من مضاعفات الرقم
: نحن تعيين اللون الأزرق إلى كل مربع في جدول الضرب الذي هو من مضاعفات الرقم 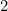 . (عدد
. (عدد 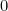 من مضاعفات
من مضاعفات 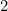 ، لذلك كل
، لذلك كل 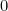 الساحات والأزرق).
الساحات والأزرق).
هنا فإننا قمنا بمد الجدول قليلا بحيث يتم تشغيله حتى عدد 15 في الاتجاه الأفقي. في الواقع، منذ جدول الضرب كامل على الأعداد الصحيحة الموجبة لانهائية على الجانبين، وسوف نستمر في قرص أبعاد الجداول في ما يلي لعرض الأنماط الناشئة أكثر وضوحا.
لاحظ أن نمط كله فوق يمكن تجميعها معا باستخدام بنة أساسية:

لبنة أساسية يحتوي على 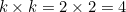 خلايا جدول الضرب. الساحات التي حددها الخلايا البيضاء في نمط تتكون من
خلايا جدول الضرب. الساحات التي حددها الخلايا البيضاء في نمط تتكون من
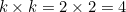 خلايا جدول الضرب. الساحات التي حددها الخلايا البيضاء في نمط تتكون من
خلايا جدول الضرب. الساحات التي حددها الخلايا البيضاء في نمط تتكون من![\ [(ك-1) ^ 2 = (1/2) ^ 2 = 1 \]](https://plus.maths.org/MI/db5d24bd1132ea957603690494c23003/images/img-0002.png) |
الخلايا.
وفيما يلي اثنين من أكثر الصور التي مضاعفات عدد  تم باللون الأزرق. يمكن أن أقول لكم ما قيمة
تم باللون الأزرق. يمكن أن أقول لكم ما قيمة  هي في كل حالة؟ يمكن أن أقول لكم ما هي لبنات البناء الأساسية، كم من الخلايا التي تحتوي عليها، وعدد الخلايا تشكل الساحات التي حددها الخلايا البيضاء؟ يمكنك الرد على إجاباتك في مجال التعليق أدناه - في حال كنت لا يمكن أن تعمل بها، وسنقوم بنشر الإجابات في غضون بضعة أسابيع.
هي في كل حالة؟ يمكن أن أقول لكم ما هي لبنات البناء الأساسية، كم من الخلايا التي تحتوي عليها، وعدد الخلايا تشكل الساحات التي حددها الخلايا البيضاء؟ يمكنك الرد على إجاباتك في مجال التعليق أدناه - في حال كنت لا يمكن أن تعمل بها، وسنقوم بنشر الإجابات في غضون بضعة أسابيع.
 تم باللون الأزرق. يمكن أن أقول لكم ما قيمة
تم باللون الأزرق. يمكن أن أقول لكم ما قيمة 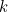 هي في كل حالة؟ يمكن أن أقول لكم ما هي لبنات البناء الأساسية، كم من الخلايا التي تحتوي عليها، وعدد الخلايا تشكل الساحات التي حددها الخلايا البيضاء؟ يمكنك الرد على إجاباتك في مجال التعليق أدناه - في حال كنت لا يمكن أن تعمل بها، وسنقوم بنشر الإجابات في غضون بضعة أسابيع.
هي في كل حالة؟ يمكن أن أقول لكم ما هي لبنات البناء الأساسية، كم من الخلايا التي تحتوي عليها، وعدد الخلايا تشكل الساحات التي حددها الخلايا البيضاء؟ يمكنك الرد على إجاباتك في مجال التعليق أدناه - في حال كنت لا يمكن أن تعمل بها، وسنقوم بنشر الإجابات في غضون بضعة أسابيع.

مضاعفات متعددة من أرقام متتالية
ويبرز نمط أكثر إثارة للاهتمام إذا استخدمنا مضاعفات متعددة، والمقابلة لها، وألوان متعددة. في الشكل التالي، والأرقام التي هي مضاعفات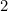 الملونة الحمراء، وتلك التي هي مضاعفات
الملونة الحمراء، وتلك التي هي مضاعفات 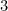 وبرتقالية اللون (مع البرتقال أخذ الأسبقية على أحمر في حالة من مضاعفات على حد سواء
وبرتقالية اللون (مع البرتقال أخذ الأسبقية على أحمر في حالة من مضاعفات على حد سواء 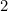 و
و 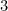 ، أي مضاعفات
، أي مضاعفات 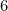 ).
).
وهذا يعطي نمط التالي.

الجمال الخفية للجداول الضرب
![الجمال الخفية للجداول الضرب]() Reviewed by . blogmathappily
on
4:25 م
Rating:
Reviewed by . blogmathappily
on
4:25 م
Rating:
