تطبيقات المتتاليات في الحياة
https://plus.maths.org/content/sites/plus.maths.org/files/articles/2013/fibonacci/nautiluscutawaylogarithmicspiral.jpgالمقدمة من plusadmin في 4 نوفمبر 2013


الذي هو مجرد حكم لتوليد أرقام فيبوناتشي: إضافة الماضيين للحصول على التالي. وبعد ذلك من خلال ستجد أنه بعد 12 شهرا (أو 1 سنة)، سيكون هناك 233 أزواج من الأرانب.




فيبوناتشي هي واحدة من أكثر الأسماء شهرة في الرياضيات. وهذا من شأنه أن يشكل مفاجأة ليوناردو بيسانو، عالم الرياضيات ونحن نعلم الآن بهذا الاسم. وانه ربما كان يفاجأ بنفس القدر أنه قد خلدت في تسلسل الشهير - 0، 1، 1، 2، 3، 5، 8، 13، ... - وليس من أجل ما يعتبر له أكبر بكثير التحصيل الرياضي - مساعدة من أجل الترويج لنظامنا عدد المعاصر في العالم الناطق باللغة اللاتينية.
تركت الامبراطورية الرومانية أوروبا مع نظام الأرقام الرومانية التي لا نزال نرى، من بين أماكن أخرى، في إشعارات حقوق التأليف والنشر بعد الأفلام والبرامج التلفزيونية (2013 غير MMXIII). لم ينزحوا الأرقام الرومانية حتى منتصف ال13 الميلادي، وكتاب ليوناردو بيسانو و يبر العدادات (والتي تعني "كتاب الحسابات")، كان واحدا من الكتب الغربية الأولى لوصف الاستعاضة عنها في نهاية المطاف.

c1175-1250 ليوناردو فيبوناتشي.
ولد ليوناردو بيسانو في أواخر القرن الثاني عشر في بيزا، إيطاليا: أشار بيسانو باللغة الإيطالية أنه كان من بيزا، في نفس الطريقة Mancunian احسن يشير إلى أن أنا من مانشستر. وكان والده تاجرا دعا غولييلمو بوناتسيو وانها بسبب اسم والده الذي أصبح ليوناردو بيسانو المعروفة باسم فيبوناتشي. في وقت لاحق قرون، عندما كان العلماء يدرسون نسخ مكتوبة بخط اليد من ليبر العدادات (كما تم نشره قبل اختراع الطباعة)، ويساء تفسيرها جزء من العنوان - "Filius المقابل Bonacci" يعني "ابن Bonaccio" - كما لقبه، وكان فيبوناتشي مولود.
فيبوناتشي (ونحن سوف تحمل على الدعوة وسلم) قضى طفولته في شمال أفريقيا حيث كان والده ضابط الجمارك. تلقى تعليمه على يد المغاربة وسافر على نطاق واسع في البربري (الجزائر)، وأرسل في وقت لاحق في رحلات عمل إلى مصر وسوريا واليونان وصقلية وبروفانس. في 1200 عاد الى بيزا واستخدام المعرفة التي اكتسبها في أسفاره لكتابة يبر العدادات (نشرت في 12022) في عرض فيه العالم الناطقة باللغة اللاتينية لنظام الأرقام العشرية.الفصل الأول من الجزء 1 يبدأ:
"هذه هي الأرقام تسعة من الهنود: 9 8 7 6 5 4 3 2 1. مع هذه الأرقام التسعة، ومع هذا التوقيع 0 أي في العربية يسمى zephirum، أي عدد يمكن أن تكون مكتوبة، كما سيظهر."
وجاء ايطاليا في ذلك الوقت تتكون من مدن ومناطق صغيرة مستقلة، وهذا أدى إلى استخدام أنواع كثيرة من الأوزان وأنظمة المال. وكان التجار لتحويل من واحد إلى آخر كلما المتبادلة بين هذه النظم. كتب فيبوناتشي يبر العدادات لهؤلاء التجار، مليئة المشاكل العملية وعملت الأمثلة التي تبين كيف ببساطة يمكن أن يتم الحسابات التجارية والرياضية مع هذا النظام رقم جديد مقارنة مع الأرقام الرومانية غير عملي. وكان أثر كتاب فيبوناتشي باعتبارها بداية انتشار الأرقام العشرية أعظم إنجاز له الرياضي. ومع ذلك، فيبوناتشي تذكرت أفضل لتسلسل معين من الأرقام التي ظهرت على سبيل المثال في ليبر العدادات .

صفحة من ليبر العدادات فيبوناتشي من الببليوتيكا ناسيونالي دي فلورنسا تبين تسلسل فيبوناتشي (في المربع على اليمين) ".
المشكلة مع الأرانب
واحدة من المشاكل الرياضية فيبوناتشي التحقيق في يبر العدادات وحول كيفية الأرانب سريعة يمكن أن تولد في ظروف مثالية. لنفترض أن الزوج المولود حديثا من الأرانب وذكر واحد، واحدة من الإناث، وضعت في حقل. الأرانب هي قادرة على التزاوج في عمر شهر واحد حتى أنه في نهاية الشهر الثاني الأنثى يمكن أن تنتج زوج آخر من الأرانب. لنفترض أن لدينا الأرانب يموت أبدا وأن الأنثى تنتج دائما زوج واحد جديد (ذكر واحد، أنثى واحدة) كل شهر من الشهر الثاني على. اللغز التي شكلت فيبوناتشي كان ... كم عدد أزواج سوف يكون هناك في سنة واحدة؟
- في نهاية الشهر الأول، تتزاوج، ولكن لا يزال هناك فقط 1 زوج.
- في نهاية الشهر الثاني تنتج الأنثى زوج جديد، وحتى الآن هناك 2 أزواج من الأرانب.
- في نهاية الشهر الثالث، والأنثى الأصلية تنتج الزوج الثاني، مما يجعل 3 أزواج في كل شيء.
- في نهاية الشهر الرابع، والأنثى الأصلية أنتجت بعد زوج جديد آخر، والأنثى ولدت قبل شهرين أنتجت أول زوج لها أيضا، مما 5 أزواج.
الآن تخيل أن هناك 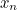 أزواج من الأرانب بعد
أزواج من الأرانب بعد 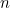 أشهر. عدد أزواج في شهر و
أشهر. عدد أزواج في شهر و 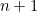 سيتم
سيتم 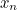 (في هذه المشكلة، الأرانب يموت أبدا)، بالإضافة إلى عدد من أزواج المولود الجديد. لكن أزواج جديدة يولدون فقط لأزواج القديمة 1 شهر على الأقل، لذلك سيكون هناك
(في هذه المشكلة، الأرانب يموت أبدا)، بالإضافة إلى عدد من أزواج المولود الجديد. لكن أزواج جديدة يولدون فقط لأزواج القديمة 1 شهر على الأقل، لذلك سيكون هناك 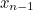 أزواج جديدة. اذا لدينا
أزواج جديدة. اذا لدينا
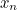 أزواج من الأرانب بعد
أزواج من الأرانب بعد 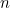 أشهر. عدد أزواج في شهر و
أشهر. عدد أزواج في شهر و 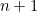 سيتم
سيتم 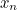 (في هذه المشكلة، الأرانب يموت أبدا)، بالإضافة إلى عدد من أزواج المولود الجديد. لكن أزواج جديدة يولدون فقط لأزواج القديمة 1 شهر على الأقل، لذلك سيكون هناك
(في هذه المشكلة، الأرانب يموت أبدا)، بالإضافة إلى عدد من أزواج المولود الجديد. لكن أزواج جديدة يولدون فقط لأزواج القديمة 1 شهر على الأقل، لذلك سيكون هناك 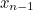 أزواج جديدة. اذا لدينا
أزواج جديدة. اذا لدينا![\ [X_ {ن + 1} = X_ ن + X_ {ن 1} \]](https://plus.maths.org/MI/56b4da3e8e9bba0d29c0f9a56d6866ce/images/img-0005.png) |
النحل أفضل
المشكلة أرنب ومن الواضح مفتعلة جدا، ولكن لم يحدث متتالية فيبوناتشي في السكان الحقيقي. توفر النحل مثالا على ذلك. في مستعمرة نحل العسل هناك واحد من الإناث خاصة تسمى الملكة. الإناث غيرها من النحل العامل الذي، على عكس ملكة النحل وإنتاج لا البيض. النحل الذكور القيام بأي عمل وتسمى النحل بدون طيار.
ويتم إنتاج الذكور من البيض غير مخصبة الملكة، لذلك ذكور النحل ليس لها سوى الأم ولكن لا أب. ويتم إنتاج جميع الإناث عند الملكة قد تزاوج مع ذكر وبحيث يكون اثنين من الآباء.وعادة ما تنتهي الإناث على النحو الشغالات ولكن يتم تغذية بعض بمادة خاصة تسمى غذاء ملكات النحل مما يجعلها تنمو لتصبح ملكات معدة للتفجير لبدء مستعمرة جديدة عندما تشكل النحل سرب وترك وطنهم (خلية) بحثا عن مكان لبناء عش جديد. حتى النحل الإناث واثنين من الآباء والأمهات، من الذكور والإناث في حين ذكور النحل لها فقط أحد الوالدين، أنثى.

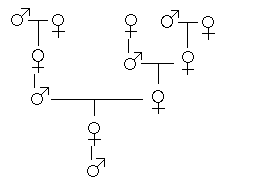
دعونا ننظر إلى شجرة عائلة النحل بدون طيار الذكور.
لديه 1 الأم، والإناث.
لديه 2 الأجداد، حيث أن والدته أبوين، ذكرا وأنثى.
لديه 3 الأجداد كبيرة: كانت جدته أبوين ولكن كان جده احد فقط.
كم عدد رائعة لكبيرة الأجداد التي كانت لديه؟
مرة أخرى نرى أرقام فيبوناتشي:
لديه 2 الأجداد، حيث أن والدته أبوين، ذكرا وأنثى.
لديه 3 الأجداد كبيرة: كانت جدته أبوين ولكن كان جده احد فقط.
كم عدد رائعة لكبيرة الأجداد التي كانت لديه؟
مرة أخرى نرى أرقام فيبوناتشي:
| رقم ال | الآباء | الجد والجدة | العظمى- الأجداد | عظيم-العظمى- الأجداد | عظيم، عظيم، العظمى- الأجداد |
| من نحلة MALE | 1 | 2 | 3 | 5 | 8 |
| من نحلة أنثى | 2 | 3 | 5 | 8 | 13 |
اللوالب وقذائف

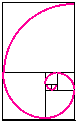
السكان النحل ليست هي المكان الوحيد في الطبيعة التي تحدث فيها أرقام فيبوناتشي، فإنها تظهر أيضا في أشكال جميلة من الأصداف. لرؤية هذا، دعونا بناء صورة البدء مع اثنين من مربعات صغيرة الحجم 1 بجانب بعضها البعض. على رأس كل من هذه رسم مربع من حجم 2 (= 1 + 1). يمكننا الآن رسم مربع جديد - لمس كل من واحدة من الساحات وحدة وآخر مربع من الجانب 2 - وذلك بعد الجانبين 3 وحدات طويلة؛ ثم آخر لمس كل من 2 مربع و3-مربع (التي لديها جوانب من 5 وحدات). يمكننا الاستمرار مضيفا الساحات حول الصورة، كل مربع جديد وجود الجانب الذي دام كمجموع الجانبين أحدث اثنين مربع و. هذه مجموعة من المستطيلات التي الجانبين هما أرقام فيبوناتشي المتعاقبة في الطول، والتي تتكون من المربعات مع الجانبين وهي عبارة عن أرقام فيبوناتشي، فإننا سوف استدعاء مستطيلات فيبوناتشي .

إذا كنا الآن رسم ربع دائرة في كل مربع، يمكننا بناء نوع من دوامة. دوامة ليست دوامة الرياضية الحقيقية (منذ أنه يتكون من الشظايا التي هي أجزاء من الدوائر ولا يذهب على الحصول على أصغر وأصغر) وإنما هو تقريب جيد لنوع من دوامة التي لا تظهر في كثير من الأحيان في الطبيعة. وتعتبر هذه اللوالب في شكل أصداف القواقع والأصداف البحرية. الصورة أدناه من شريحة واسعة من قذيفة نوتيلوس يظهر منحنى دوامة من قذيفة والغرف الداخلية أن هذا الحيوان استخدامه يضيف على أنها تنمو. توفر غرف الطفو في الماء.

تظهر أرقام فيبوناتشي أيضا في النباتات والزهور. بعض فرع النباتات في مثل هذه الطريقة التي لديهم دائما عدد فيبوناتشي من النقاط المتنامية. الزهور غالبا ما يكون عدد فيبوناتشي من بتلات، يمكن أن يكون البابونج 34، 55 أو حتى ما يصل الى 89 بتلات!
A مظهر جميل وخصوصا من أرقام فيبوناتشي هو في اللوالب من البذور في الرأس البذور. في المرة القادمة التي ترى عباد الشمس، والنظر في الترتيبات من البذور في وسطها. يبدو أنها المتصاعد الخارج على حد سواء إلى اليسار واليمين.
 |  |  |
على حافة هذا صورة لعباد الشمس، وإذا كنت تعول تلك المنحنيات البذور المتصاعد إلى اليسار كما تذهب إلى الخارج، وهناك 55 اللوالب. في نفس النقطة هناك 34 اللوالب من البذور المتصاعد إلى اليمين. وأبعد قليلا نحو الوسط ويمكنك الاعتماد 34 اللوالب إلى اليسار و 21 اللوالب إلى اليمين. زوج من الأرقام (عد اللوالب التقويس اليسرى والتقويس اليمين) هي (دائما تقريبا) الجيران في سلسلة فيبوناتشي.
والشيء نفسه يحدث في كثير من البذور ورؤساء الزهور في الطبيعة. السبب يبدو أن هذا الترتيب يشكل التعبئة المثلى من البذور بحيث، مهما كانت كبيرة الرأس البذور، وكانت معبأة بشكل موحد في أي مرحلة، كل بذور يجري نفس الحجم، لا الزحام في وسط وليس أيضا متفرق عند الحواف.
يبدو طبيعة استخدام نفس النمط لترتيب بتلات حول حافة زهرة ووضع الأوراق جولة الجذعية. ما هو أكثر من ذلك، كل هذه المحافظة كفاءتها مع استمرار النبات على النمو وهذا هو الكثير أن نسأل من عملية واحدة! هكذا فقط كيف تنمو النباتات للحفاظ على هذه المثالية من التصميم؟
نمو الذهبي
وقد أظهرت علماء النبات أن النباتات تنمو من مجموعة صغيرة واحدة من الخلايا الحق في غيض من أي النباتات التي تنمو، ودعا النسيج الإنشائي . هناك النسيج الإنشائي منفصل في نهاية كل فرع أو غصين حيث تتشكل خلايا جديدة. تشكلت مرة واحدة، فإنها تنمو في الحجم، ولكن تتشكل خلايا جديدة فقط في هذه النقاط المتنامية. خلايا في وقت سابق من أسفل الساق توسيع وحتى يرتفع نقطة المتنامية. أيضا، تنمو هذه الخلايا بطريقة لولبية: كما لو يتحول النسيج الإنشائي من زاوية، وتنتج خلية جديدة، وينتقل مرة أخرى من قبل نفس الزاوية، وتنتج خلية جديدة، وهلم جرا. ثم قد تصبح هذه الخلايا البذور، صفحة جديدة، فرع جديد، أو ربما على زهرة تصبح بتلات والأسدية.

أوراق مرقمة هنا بدوره - كل هو بالضبط 0.618 منعطفا في اتجاه عقارب الساعة (222.5 درجة) عن سابقتها.
الشيء المدهش هو أن زاوية ثابتة واحدة من دوران يمكن أن تنتج التصميم الأمثل مهما كانت كبيرة ينمو النبات. مبدأ أن زاوية واحدة تنتج عبوات موحدة بغض النظر عن مدى يظهر النمو من ذلك بكثير وكان يشتبه في وقت مبكر من القرن الماضي ولكن ثبت فقط رياضيا في عام 1993 من قبل ستيفان دوادي و إيف كودر ، واثنين من علماء الرياضيات الفرنسية.مما يجعل 0.618 منعطفا قبل إنتاج البذور جديد (أو ورقة، البتلة، الخ) تنتج التعبئة المثلى للبذور بغض النظر عن حجم الرأس البذور. ولكن أين هذا الرقم السحري 0.618 تأتي من؟
النسبة الذهبية
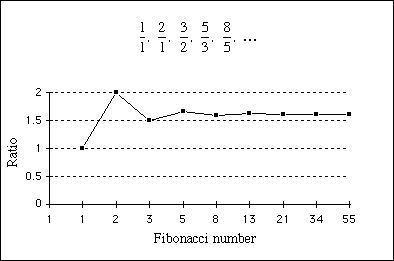
وإذا أخذنا نسبة رقمين متتاليين في سلسلة فيبوناتشي، وتقسيم كل من الرقم قبل ذلك، سوف نجد أن السلسلة التالية من الأرقام:
1/1 = 1، 2/1 = 2، 3/2 = 1.5، 5/3 = 1.666 ...، 8/5 = 1.6، 13/8 = 1.625، 21/13 = 1.61538 ...
إذا كنت رسم بياني لهذه القيم سترى أن يبدو أنها تميل إلى الحد الذي نسميه النسبة الذهبية (المعروفة أيضا باسم عدد الذهبي و المقطع الذهبي ).

نسبة من حيث فيبوناتشي المتعاقبة.
أنه يحتوي على قيمة 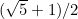 (حوالي 1.618034) وغالبا ما يمثله الحرف اليوناني فاي، كما هو مكتوب
(حوالي 1.618034) وغالبا ما يمثله الحرف اليوناني فاي، كما هو مكتوب 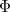 . قيمة وثيقة الصلة التي نكتب كما
. قيمة وثيقة الصلة التي نكتب كما 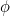 وفاي صغيرة، هو مجرد جزء عشري فاي، وهي 0.618034 ... (
وفاي صغيرة، هو مجرد جزء عشري فاي، وهي 0.618034 ... ( 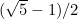 )، الرقم الذي يمثل اللوالب في seedheads والترتيبات من الأوراق في العديد من النباتات. ولكن لماذا لا نرى فاي في العديد من النباتات؟
)، الرقم الذي يمثل اللوالب في seedheads والترتيبات من الأوراق في العديد من النباتات. ولكن لماذا لا نرى فاي في العديد من النباتات؟
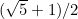 (حوالي 1.618034) وغالبا ما يمثله الحرف اليوناني فاي، كما هو مكتوب
(حوالي 1.618034) وغالبا ما يمثله الحرف اليوناني فاي، كما هو مكتوب 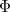 . قيمة وثيقة الصلة التي نكتب كما
. قيمة وثيقة الصلة التي نكتب كما 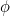 وفاي صغيرة، هو مجرد جزء عشري فاي، وهي 0.618034 ... (
وفاي صغيرة، هو مجرد جزء عشري فاي، وهي 0.618034 ... ( 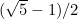 )، الرقم الذي يمثل اللوالب في seedheads والترتيبات من الأوراق في العديد من النباتات. ولكن لماذا لا نرى فاي في العديد من النباتات؟
)، الرقم الذي يمثل اللوالب في seedheads والترتيبات من الأوراق في العديد من النباتات. ولكن لماذا لا نرى فاي في العديد من النباتات؟
وفاي (1.618034 ...) العدد، وبالتالي أيضا PHI (0.618034 ...)، هي أرقام غير منطقية: لا يمكن كتابة ككسر بسيط. دعونا نرى ماذا سيحدث لو النسيج الإنشائي في رأس البذور تحولت بدلا من ذلك من قبل بعض عدد بساطة، على سبيل المثال جزء 1/2. بعد لفتين من خلال نصف دائرة سنكون العودة إلى حيث تم إنتاج البذرة الأولى. مع مرور الوقت، وتحول بمقدار نصف بدوره بين البذور من شأنها أن تنتج رئيس البذور مع اثنين من الأسلحة يشع من نقطة مركزية، وترك الكثير من مساحة مهدرة.
رأس البذور التي تنتجها 0.5 = 1/2 يتحول بين البذور: بذور بديلة حتى خط.
| 
رأس البذور التي تنتجها 0.48 = 12/25 يتحول بين البذور: بذور شكل ذراعين الدوارة.
| 
رأس البذور التي تنتجها 0.6 = 3/5 يتحول بين البذور: شكل بذور 5 الأسلحة على التوالي.
|

بي يتحول بين البذور تنتج سبعة الأسلحة المتصاعد
شيئا من هذا القبيل يحدث لأي جزء بسيط الآخر من منعطفا: تنمو البذور في الأذرع الحلزونية التي تترك الكثير من المسافة التي تفصل بينهما (عدد الأسلحة هو مقام الكسر). وبالتالي فإن أفضل قيمة ليتحول بين البذور سيكون عدد غير عقلاني. ولكن ليس أي رقم غير منطقي وسوف نفعل. على سبيل المثال، رئيس البذور التي تم إنشاؤها باستخدام بي يتحول في البذور يبدو أن سبعة الأسلحة المتصاعد من البذور. وذلك لأن 22/7 هو تقريب عقلانية جيد جدا بي.
ما هو مطلوب من أجل عدم إضاعة الفضاء هو عدد غير منطقي أن لا يقترب بشكل جيد من قبل عدد العقلاني. واتضح أن فاي (1.618034 ...) وفاي في عشري جزء (0.618034 ...) هي "الأكثر عقلانية" جميع أرقام غير منطقية. (يمكنك معرفة السبب فيالفوضى في الأراضي رقم: الحياة السرية لاستمرار كسور .) وهذا هو السبب في مطلع فاي يعطي التعبئة المثلى من البذور ويترك في النباتات. وهذا ما يفسر أيضا لماذا تظهر أرقام فيبوناتشي في الترتيبات ورقة وحيث أن عدد اللوالب في seedheads. أرقام فيبوناتشي المجاورة تعطي أفضل تقريبية لنسبة الذهبية. وهم يتناوبون في كونه مقام تقريبية وتحديد عدد أو اللوالب مع زيادة رؤوس البذور في الحجم.
كيف العديد من النباتات اكتشاف هذا العدد جميلة ومفيدة، فاي؟ ومن الواضح أن ليس من حل الرياضيات كما فعل فيبوناتشي. بدلا من ذلك نحن نفترض أن، كما أن نسبة أعداد فيبوناتشي المتعاقبة يستقر في نهاية المطاف على النسبة الذهبية، وتطور تدريجيا تسديد على العدد الصحيح أيضا. إرث ليوناردو بيسانو، ويعرف أيضا باسم فيبوناتشي، وتقع في قلب كل زهرة، وكذلك في قلب نظام الأرقام لدينا.
تطبيقات المتتاليات في الحياة
![تطبيقات المتتاليات في الحياة]() Reviewed by . blogmathappily
on
4:33 م
Rating:
Reviewed by . blogmathappily
on
4:33 م
Rating:
