الباي ( π )

باي ( π )

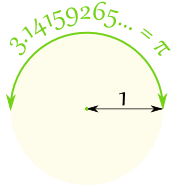رسم دائرة مع دائرة نصف قطرها من 1 الطريقة نصف المسافة حول الدائرة هي 3.14159265 ... عدد المعروفة باسم باي

أو رسم دائرة مع قطر (على طول الطريق عبر الدائرة) من 1 ثم محيط (على طول الطريق حول الدائرة) هو باي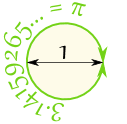

لذا باي (الرمز هو الحرف اليوناني π ) هي: نسبة محيط إلى القطر من الدائرة.

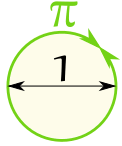
لمساعدتك على تذكر ما يعني
مجرد رسم هذا المخطط.

 

رسم دائرة، أو استخدام شيء دائري مثل طبق من ذهب.

قياس حول حافة (في محيط ):

حصلت على 82 سم

قياس عبر الدائرة ( قطر ):

حصلت على 26 سم

يقسم:

82 سم / 26 سم = 3.1538 ...

وهذا هو قاب قوسين أو π . ربما لو كنت قياس أكثر دقة؟

سيارة

في الواقع π تساوي تقريبا:

+3.14159265358979323846 ...

الأرقام المضي قدما وعلى مع أي نمط. π تم احتساب لأكثر من كوادريليون المنازل العشرية ومازال هناك أي نمط  للأرقام

مثال: أنت تمشي حول دائرة والتي يبلغ قطرها 100 متر، إلى أي مدى كنت قد مشى؟

مشى مسافة		= محيط
		= π × 100 م
		= 314.159 ... م
		= 314 م (إلى أقرب م)

تقريب

A تقريب سريعة وسهلة ل π هو 22/7

22/7 = 3.1428571 ...

ولكن كما ترون، 22/7 هو ليس صحيحا تماما . في الواقع π ليس مساويا لنسبة أي رقمين، مما يجعله عدد غير نسبي .

A تقريب أفضل (ولكن لا يزال لا بالضبط) هو:

355/113 = 3.1415929 ...
(اعتقد "113355"، ثم تقسيم "355" من قبل "113")

تذكر أن سيارة

أنا عادة فقط تذكر "3.14159"، ولكن يمكنك أيضا الاعتماد على خطابات:

"ربما أكون قد وعاء كبير من زبدة اليوم" 
3 1 4 1 5 9 2 6 5

100 المنازل العشرية

هنا هو π مع أول 100 عشريين:

3.14159265358979323846264338327950288 4197169399375105820974944592307816 4062862089986280348253421170679 ...

 

هناك العديد من الأساليب الخاصة المستخدمة لحساب π وهنا هو واحد يمكنك أن تجرب نفسك: يطلق عليها سلسلة Nilakantha (بعد عالم رياضيات الهنود الذين عاشوا في السنوات 1444-1544).
وغني إلى الأبد، ولها هذا النمط:

3 + 4 2 × 3 × 4 - 4 4 × 5 × 6 + 4 × 6 7 8 × - 4 8 × 9 × 10 + ...

(لاحظ + و - نمط، وأيضا نمط الأرقام أدناه السطور.)
أنه يعطي هذه النتائج:

مصطلح	نتيجة (12 عشرية)
1	3
2	+3.166666666667
3	+3.133333333333
4	+3.145238095238
...	... الخ! ...