الراديان

جعلت زاوية عندما نصف قطر
ومن لف الجولة دائرة:

1 راديان هو حوالي 57.2958 درجة .

لماذا "57،2958 ..." درجة؟ سنرى في لحظة.

و راديان هو مقياس النقي على أساس نصف قطر الدائرة:

راديان : زاوية جعلت عندما نأخذ نصف قطرها
، والانتهاء من جولة الدائرة.

راديان والدرجات

دعونا نرى لماذا 1 راديان تساوي 57.2958 ... درجات:

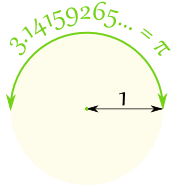
في نصف دائرة هناك π راديان ، الذي هو أيضا 180 °

وبالتالي:		π راديان	=	180 °
وبالتالي:		1 راديان	=	180 ° / π
			=	57.2958 ° ...
				(تقريبا)

للانتقال من راديان إلى درجات : ضرب من قبل 180، القسمة π

للانتقال من الدرجات إلى راديان : ضرب من قبل π ، القسمة 180

وفيما يلي جدول القيم ما يعادلها:

درجات	راديان (الدقة)	راديان (تقريبا)
30 °	π / 6	0.524
45 °	π / 4	0.785
60 °	π / 3	1.047
90 °	π / 2	1.571
180 °	π	3.142
270 درجة	3 π / 2	4.712
360 °	2 π	6.283

مثال: كم عدد راديان في دائرة كاملة ؟

تخيل أنك تقطيع قطعة من سلسلة بالضبط طول من المركز إلى محيط الدائرة ...

... كم عدد القطع التي تحتاجها للذهاب مرة واحدة في جميع أنحاء الدائرة؟

الجواب: 2 π (أو حوالي 6،283 قطعة من سلسلة).

راديان المفضل من قبل علماء الرياضيات

لأنه يعتمد راديان على فكرة نقية من "دائرة نصف قطرها التي تزرع على طول محيط "، فإنه غالبا ما يعطي نتائج بسيطة وطبيعية عند  استخدامها في الرياضيات.

على سبيل المثال ، أن ننظر في وظيفة شرط لقيم صغيرة جدا:

س (راديان)	1	0.1	0.01	0.001
الخطيئة (خ)	0.8414710	0.0998334	0.0099998	0.0009999998

لقيم صغيرة جدا. "س" و "الخطيئة (خ)" هي نفسها تقريبا
(طالما "س" في راديان!)

سيكون هناك أمثلة أخرى من هذا القبيل كما انك تعلم المزيد عن الرياضيات.

استنتاج

لذا، درجة هي أسهل للاستخدام في العمل اليومي، ولكن راديان أفضل بكثير للرياضيات.