حتى في تناول الطعام والشراب و التأكد من انها آمنة نستخدم الرياضيات
تناول الطعام والشراب ومرح: التأكد من انها آمنة
معظم الرياضيين لديهم مشكلة دائمة عندما يطلب منهم لتبرير وجودهم في الحزب. كيف يمكن أن يكون الرياضيات من أي استخدام، هو سؤال شائع. ومع ذلك، في سياق طرفا فيها، حيث أننا نعلم جميعا أن الطعام الجيد أمر حيوي والرياضيات هي عنصر أساسي. في الواقع، الرياضيات هي ذات أهمية حيوية لصناعة المواد الغذائية والعديد من عمليات التعامل مع الغذاء. من المزرعة إلى المائدة، ومن شوكة إلى (آسف لتكون النفط الخام) المجاري والرياضيات هناك. وهذا ما يفسر ونماذج العمليات التي تحكم الانتاج الآمن والتخزين، والاختبار، والنقل، والطبخ، والأكل والهضم من المواد الغذائية (بل والعقاقير الدوائية). وعلى وجه الخصوص أنه يساعد تقرر ما إذا كانت وكيف أنها آمنة لطهي الطعام، وتناول الطعام وهضم المواد الغذائية.

هناك الكثير من الرياضيات في الشوكولاته وأنها ذاقت جيدة، أيضا!
في هذه السلسلة من مادتين سوف يكون لي نظرة على اثنين من الطرق التي الرياضيات تأتي في الغذاء، وخصوصا في سلامة الأغذية والصحة. في هذه المقالة سوف ننظر في كيفية الرياضيات يمكن أن تخبرنا الطريق الأسلم لطهي الطعام (في فرن الميكروويف). و مادة أخرى يأخذ الغوص في أعمال رائحة كريهة بدلا من هضم الطعام، وكيفية تطبيق مجنون من نظرية الفوضى يبين أفضل طريقة لهضم المخدرات الطبية.
لعل القارئ لطيف أعتقد أن هذا هو كل قليلا من مضيعة للوقت الجميع وليس تطبيق جدي للعلوم والتأمل في البسكويت المتواضع. "فما"، وقال تطبيق جميل الرياضيات يساعد على التنبؤ متى الكراك البسكويت، وبالتالي يمكن أن تقلل من فرصة لهم تكسير عندما صنعت منها. اليوم برنامج المقابلة عندما واجه مع هذه حقيقة مذهلة. حسنا، فإنه يتحول ذلك إلى أن صناعة البسكويت والصناعات الغذائية الإضافية توظف 1.5 مليون نسمة، وتمثل 15٪ من إجمالي الإنتاج الصناعي في المملكة المتحدة وسنويا تساهم أكثر من £ 1BN لاقتصاد المملكة المتحدة، وتكون صادقة مع نفسك، هل شراء علبة من البسكويت متصدع؟
طهي الطعام في المايكرويف

فرن الميكروويف المحلي أثار الوضع مع أربعة تحقيقات درجة الحرارة المستخدمة لاختبار التنبؤات للنموذج.
مثل أي طالب (أو في الواقع من الصعب حتى أستاذ) يعرف، وسيلة شائعة للطبخ (أو على الأقل من التدفئة) الغذاء إلى استخدام طنجرة الميكروويف. في مثل طنجرة يتم إنشاء أفران ميكروويف من قبلالمغناطيسية (التي تستخدم أيضا في مجموعات الرادار) ويدخل تجويف الفرن عن طريق الدليل الموجي أو هوائي. ثم يتم تعيين الحقل الكهربائي حتى داخل الفرن الذي يضيء أي طعام وضعها هناك.الموجات الدقيقة تخترق المواد الغذائية وتغيير التوجه للجزيئات في الجزء الرطب من المواد الغذائية مما يؤدي إلى تسخين (عن طريق الاحتكاك كما تهتز جزيئات ضد جزيئات أخرى في الغذاء) من المواد الغذائية والتغيرات يترتب على ذلك من الماء في الطعام إلى بخار .
وهناك مشكلة مع هذه العملية هو أن هذا المجال يمكن أن يكون واقفا أنماط موجة، الذي يمكن أن يؤدي إلى "النقاط الباردة" المترجمة حيث مجال ضعيفة نسبيا. إذا وضعت الطعام في مكان بارد ثم درجة الحرارة قد يكون أقل هناك، وسوف يتم طهيها بشكل سيئ (انظر الشكل). وهذا له آثار كبيرة جدا على الصحة العامة.إذا كان الطعام ليست ساخنة بما فيه الكفاية، ثم البكتيريا في أنها لن يقتلوا وهذا يمكن أن يؤدي بعد ذلك إلى التسمم الغذائي الحاد. في محاولة لتجنب هذه المشكلة الطعام إما أن تكون استدارة من خلال الميدان على المناورة، أو الحقل نفسه يمكن "اثارة" باستخدام مروحة معدنية الدورية لتفريق أنماط المجال.

صورة الحرارية كاميرا من الطعام في الفرن الدوار المحلي، مما يدل على بقعة باردة متميزة في وسط الناجمة عن الحد الأدنى المحلية في المجال المغناطيسي الكهربائي اشعاعا. وهذا يمكن أن تترك لطبخ متفاوتة جدا مع عواقب خطرة.
باستخدام الرياضيات يمكننا نموذج العملية التي يتم تسخين الطعام في الفرن ومقارنة فعالية القرص الدوار والتصاميم أثارت طريقة الفرن موجة الصغرى. للقيام بذلك، ونحن بحاجة إلى القيام بثلاثة الحسابات. أولا نحن بحاجة للعثور على المجال الكهرومغناطيسي في الغذاء بسبب الموجات الدقيقة. ثانيا علينا أن نعمل كيف تسخن هذا المجال الطعام حتى. وثالثا علينا أن نعمل بها، وكم من الماء في الغذاء يتحول إلى بخار أثناء عملية الطهي. مشيرا إلى أن العديد من المواد الغذائية هي في البداية 80٪ من المياه، وهذا الأخير يشكل جزءا رئيسيا من الحساب.
الطريق الصعب
طريقة واحدة لمعالجة هذه عملية الحساب لمحاكاة حقل كهربائي ثلاثي الأبعاد الكامل من خلال حل معادلات ماكسويل للإشعاع الكهرومغناطيسي. استخدام هذا يمكننا ثم العثور على درجة الحرارة عن طريق حل مجموعة أخرى من المعادلات، و المعادلات المتوسطة التي يسهل اختراقها لمادة مرحلتين، والتي هي (عادة) مزيج من النشا والماء.
المشاكل مع هذا النهج هي أولا أن الحسابات تستغرق وقتا طويلا جدا (في كثير من الأحيان عدة ساعات!) وغالبا ما تكون غير موثوق بها ويصعب التحقق منها. وهذا يجعل من الصعب أن نرى ما يحدث عندما تختلف المعلمات في المشكلة، مثل ما إذا كان الطعام على طاولة بدوره أو يتم استخدام فرن وضع النمام. ثانيا، هذا الأسلوب يعطي نظرة المباشرة قليلا في العملية والطريقة التي تعتمد على المعلمات. ثالثا، موجة الصغرى الطبخ حساسة جدا للتغيرات صغيرة في هندسة تجويف، وشكل ونوع الطعام وحتى الرطوبة من الهواء. وهذا يعني أن أي حساب واحد قد لا تعطي بالضرورة تمثيل دقيق للمجال الكهربائي في أي فرن الموجات الدقيقة معين في أي يوم معين.
أسهل طريقة
ما هو أكثر فائدة هو حساب التمثيلي للمتوسط سلوك فئة واسعة من (المحلية) أفران الموجات الدقيقة التي تأثيرات متفاوتة على مختلف المعايير أكثر شفافية. هذا هو في كثير من الأحيان كيف يمكن لنهج النمذجة الرياضية يمكن أن تكون فعالة جدا: يمكن أن قليلا الرياضيات حل ساعات وساعات من وقت الكمبيوتر، وكذلك غالبا ما يعطي إجابة أكثر دقة.
الآن، خلافا لأسطورة شعبية وأفران ميكروويف لا طهي الطعام من الداخل. وبدلا من ذلك اختراق من الخارج ويتم امتصاصها لأنها تمر في المواد الغذائية وفقدان الطاقة لأنها تفعل ذلك.جزء من سخونة الطعام المطبوخ في فرن الميكروويف هو عادة تحت السطح. إذا كان الطعام كبيرة جدا، ثم من الداخل ويمكن الحصول على ما يقرب من أي طاقة الأمواج الصغيرة، ونتيجة لذلك التسخين المباشر قليلا. هذا هو السبب في أن الشركات المصنعة للموجة الصغرى الأطعمة cookable يصر عموما أنه بعد فترة من التدفئة في الفرن، ويحرك الطعام للتأكد من أن كل ذلك هو في درجة حرارة مماثلة.
لنموذج ما يحدث، دعونا نتصور نحن نجلس في نقطة 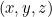 أو في منطقتنا قليلا من الطعام في وقت
أو في منطقتنا قليلا من الطعام في وقت 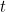 من عملية الفرن. (ونحن سوف نفكر في
من عملية الفرن. (ونحن سوف نفكر في  -coordinate كما عمق في الغذاء.) بعض مبلغ
-coordinate كما عمق في الغذاء.) بعض مبلغ 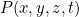 يتم نقل السلطة من مجال الميكروويف للغذاء في هذه المرحلة من الزمان والمكان. أيضا هناك بعض فقدان الحرارة بسبب التوصيل، مع حرارة نقله إلى جزيئات المجاورة. رياضيا من فقدان الحرارة وصفت من قبل التعبير
يتم نقل السلطة من مجال الميكروويف للغذاء في هذه المرحلة من الزمان والمكان. أيضا هناك بعض فقدان الحرارة بسبب التوصيل، مع حرارة نقله إلى جزيئات المجاورة. رياضيا من فقدان الحرارة وصفت من قبل التعبير
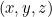 أو في منطقتنا قليلا من الطعام في وقت
أو في منطقتنا قليلا من الطعام في وقت 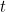 من عملية الفرن. (ونحن سوف نفكر في
من عملية الفرن. (ونحن سوف نفكر في  -coordinate كما عمق في الغذاء.) بعض مبلغ
-coordinate كما عمق في الغذاء.) بعض مبلغ 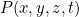 يتم نقل السلطة من مجال الميكروويف للغذاء في هذه المرحلة من الزمان والمكان. أيضا هناك بعض فقدان الحرارة بسبب التوصيل، مع حرارة نقله إلى جزيئات المجاورة. رياضيا من فقدان الحرارة وصفت من قبل التعبير
يتم نقل السلطة من مجال الميكروويف للغذاء في هذه المرحلة من الزمان والمكان. أيضا هناك بعض فقدان الحرارة بسبب التوصيل، مع حرارة نقله إلى جزيئات المجاورة. رياضيا من فقدان الحرارة وصفت من قبل التعبير![\ [ك \ nabla ^ 2 T = ك \ اليسار (\ فارك {\ الجزئي ^ 2 T (س، ص، ض، ر)} {\ جزئية س ^ 2} + \ فارك {\ الجزئي ^ 2 T (س، ذ، ض، ر)} {\ جزئية ص ^ 2} + \ فارك {\ جزئية ^ 2 T (س، ص، ض، ر)} {\ ض الجزئي ^ 2} \ اليمين)، \]](https://plus.maths.org/MI/b0cf8c0b77f6daba4a2932c00091cea9/images/img-0005.png) |
حيث 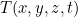 هي درجة الحرارة عند نقطة
هي درجة الحرارة عند نقطة 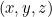 والوقت
والوقت 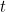 و
و 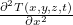 هو مشتق جزئي الثانية
هو مشتق جزئي الثانية 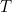 فيما يتعلق
فيما يتعلق  -coordinate (مشابه ل
-coordinate (مشابه ل 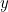 كما
كما  ). ثابت
). ثابت 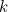 هوالموصلية الحرارية من الطعام، والذي يقيس قدرته على إجراء الحرارة.
هوالموصلية الحرارية من الطعام، والذي يقيس قدرته على إجراء الحرارة.
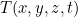 هي درجة الحرارة عند نقطة
هي درجة الحرارة عند نقطة 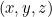 والوقت
والوقت 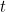 و
و 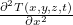 هو مشتق جزئي الثانية
هو مشتق جزئي الثانية 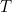 فيما يتعلق
فيما يتعلق  -coordinate (مشابه ل
-coordinate (مشابه ل 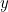 كما
كما  ). ثابت
). ثابت 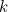 هوالموصلية الحرارية من الطعام، والذي يقيس قدرته على إجراء الحرارة.
هوالموصلية الحرارية من الطعام، والذي يقيس قدرته على إجراء الحرارة.
قوة الميكروويف 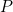 يضع الطاقة في الغذاء والتي تسخن عنه. ثم يتم فقدان الطاقة الحرارية من خلال التوصيل. معا تسخين أفران ميكروويف وفقدان الحرارة تتسبب في درجة الحرارة
يضع الطاقة في الغذاء والتي تسخن عنه. ثم يتم فقدان الطاقة الحرارية من خلال التوصيل. معا تسخين أفران ميكروويف وفقدان الحرارة تتسبب في درجة الحرارة 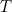 في وجهة نظرنا لتغيير مع مرور الوقت. ونعرب عن هذا التغيير في الوقت المناسب من قبل مشتق جزئي
في وجهة نظرنا لتغيير مع مرور الوقت. ونعرب عن هذا التغيير في الوقت المناسب من قبل مشتق جزئي 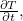 الذي نكتب
الذي نكتب 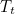 . ضرب
. ضرب 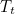 من قبل السعة الحرارية محددة
من قبل السعة الحرارية محددة  من الطعام، وهذا هو كمية الحرارة اللازمة للحصول على الطعام لتغيير درجة الحرارة، ويوازن التغير في الطاقة الحرارية المذكورة أعلاه. نحصل على المعادلة
من الطعام، وهذا هو كمية الحرارة اللازمة للحصول على الطعام لتغيير درجة الحرارة، ويوازن التغير في الطاقة الحرارية المذكورة أعلاه. نحصل على المعادلة
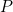 يضع الطاقة في الغذاء والتي تسخن عنه. ثم يتم فقدان الطاقة الحرارية من خلال التوصيل. معا تسخين أفران ميكروويف وفقدان الحرارة تتسبب في درجة الحرارة
يضع الطاقة في الغذاء والتي تسخن عنه. ثم يتم فقدان الطاقة الحرارية من خلال التوصيل. معا تسخين أفران ميكروويف وفقدان الحرارة تتسبب في درجة الحرارة 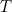 في وجهة نظرنا لتغيير مع مرور الوقت. ونعرب عن هذا التغيير في الوقت المناسب من قبل مشتق جزئي
في وجهة نظرنا لتغيير مع مرور الوقت. ونعرب عن هذا التغيير في الوقت المناسب من قبل مشتق جزئي 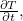 الذي نكتب
الذي نكتب 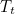 . ضرب
. ضرب 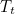 من قبل السعة الحرارية محددة
من قبل السعة الحرارية محددة  من الطعام، وهذا هو كمية الحرارة اللازمة للحصول على الطعام لتغيير درجة الحرارة، ويوازن التغير في الطاقة الحرارية المذكورة أعلاه. نحصل على المعادلة
من الطعام، وهذا هو كمية الحرارة اللازمة للحصول على الطعام لتغيير درجة الحرارة، ويوازن التغير في الطاقة الحرارية المذكورة أعلاه. نحصل على المعادلة![\ [ج T_ ر = ك \ nabla ^ 2 T + P (س، ص، ض، ر). \]](https://plus.maths.org/MI/e86889379fc8cc34032b03aa434d3dc7/images/img-0006.png) |
(إذا كانت درجة الحرارة T تصل إلى 100 درجة، ثم تغير المعادلة لأننا بحاجة إلى طاقة إضافية لتحويل الماء إلى بخار ومن ثم لتسخين البخار، ولكننا سوف تجاهل هذا التفصيل هنا.)
للعمل على درجة الحرارة 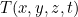 عند نقطة
عند نقطة 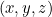 والوقت
والوقت 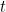 من هذه المعادلة يجب علينا أن نعرف
من هذه المعادلة يجب علينا أن نعرف 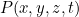 . كما لاحظ فوق، وإيجاد
. كما لاحظ فوق، وإيجاد 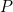 بالضبط من الصعب جدا، ولكن تقريب جيد جدا ويمكن الاطلاع أفران إما مع وضع النمام أو المناورة. ويظهر هذا التقارب الذي طالما الطعام كنت تسخين أكبر من 2CM في قطر، وعموما هذا المجال يضمحل بشكل كبير لأنها تخترق الطعام.
بالضبط من الصعب جدا، ولكن تقريب جيد جدا ويمكن الاطلاع أفران إما مع وضع النمام أو المناورة. ويظهر هذا التقارب الذي طالما الطعام كنت تسخين أكبر من 2CM في قطر، وعموما هذا المجال يضمحل بشكل كبير لأنها تخترق الطعام.
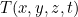 عند نقطة
عند نقطة 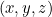 والوقت
والوقت 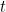 من هذه المعادلة يجب علينا أن نعرف
من هذه المعادلة يجب علينا أن نعرف 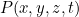 . كما لاحظ فوق، وإيجاد
. كما لاحظ فوق، وإيجاد 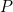 بالضبط من الصعب جدا، ولكن تقريب جيد جدا ويمكن الاطلاع أفران إما مع وضع النمام أو المناورة. ويظهر هذا التقارب الذي طالما الطعام كنت تسخين أكبر من 2CM في قطر، وعموما هذا المجال يضمحل بشكل كبير لأنها تخترق الطعام.
بالضبط من الصعب جدا، ولكن تقريب جيد جدا ويمكن الاطلاع أفران إما مع وضع النمام أو المناورة. ويظهر هذا التقارب الذي طالما الطعام كنت تسخين أكبر من 2CM في قطر، وعموما هذا المجال يضمحل بشكل كبير لأنها تخترق الطعام.
ونتيجة لذلك فإنه من الممكن استخدام وصفا أبسط بكثير من الحقل الكهربائي في معادلة المحتوى الحراري عما قدمته حل كامل للمعادلات ماكسويل. هذا يأخذ شكل
![\ [ج T_ ر = ك \ nabla ^ 2 T + P ه ^ {- س / د}. \]](https://plus.maths.org/MI/d5b4cbe6a1e8703b617aa12a57e5f413/images/img-0001.png) |
هنا 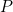 هي قوة طاقة الميكروويف على السطح من المواد الغذائية (والذي هو أسهل لحساب من
هي قوة طاقة الميكروويف على السطح من المواد الغذائية (والذي هو أسهل لحساب من 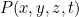 )،
)،  هي المسافة في هذا المجال و
هي المسافة في هذا المجال و 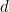 غير ثابت، ودعا عمق الاختراق. انها طول أكثر من التي تبدأ الموجات الدقيقة إلى الحصول على استيعابها بقوة، وهي عبارة عن 8MM.
غير ثابت، ودعا عمق الاختراق. انها طول أكثر من التي تبدأ الموجات الدقيقة إلى الحصول على استيعابها بقوة، وهي عبارة عن 8MM.
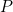 هي قوة طاقة الميكروويف على السطح من المواد الغذائية (والذي هو أسهل لحساب من
هي قوة طاقة الميكروويف على السطح من المواد الغذائية (والذي هو أسهل لحساب من 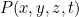 )،
)،  هي المسافة في هذا المجال و
هي المسافة في هذا المجال و 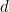 غير ثابت، ودعا عمق الاختراق. انها طول أكثر من التي تبدأ الموجات الدقيقة إلى الحصول على استيعابها بقوة، وهي عبارة عن 8MM.
غير ثابت، ودعا عمق الاختراق. انها طول أكثر من التي تبدأ الموجات الدقيقة إلى الحصول على استيعابها بقوة، وهي عبارة عن 8MM.
هذا هو معادلة نتمكن من حل بالضبط، وذلك باستخدام تقنية رياضية المعروفة باسم تحليل سلسلة فورييه (معرفة المزيد في بودكاست اصطياد موجات ). ومع ذلك، فمن السهل أن استخدام التقريب العددي في حل هذه المعادلات مبسطة. يمكن العثور على مثل هذه الحلول بشكل سريع جدا على جهاز كمبيوتر سطح المكتب. بالمقارنة مع القيم التجريبية من كل من درجة الحرارة ونسبة الرطوبة هذه الحلول دقيقة من المستغرب، نظرا لتقريبية التي يتم إجراؤها، وتعطي الثقة في استخدام نموذج لمزيد من حسابات التصميم. هو مزيج من الرياضيات، الطرق العددية، والنمذجة البدني ويتوخى الحذر في استخدام البيانات التجريبية التي تجعل هذا النهج كله ناجحة. إنها مثال نموذجي من مزيج من الأفكار التي يجب أن تكون مجتمعة للقيام فعالة الرياضيات التطبيقية الصناعية.
اختبار نموذج
سيكون لدينا الآن نظرة على بعض النتائج. في الأرقام التالية نقدم لك مجموعة من النتائج لقياس درجة حرارة المواد الغذائية النشوية رطبة ساخنة تقاس أربعة تحقيقات (والتي يمكنك ان ترى على صورة للفرن الميكروويف). وأول هذه التحقيقات هو في الخارج من المواد الغذائية، ومن ثم ينتقلون إلى الداخل بحيث التحقيق الرابع هو في وسط الطعام.
تظهر خطوط زرقاء نتائج الكثير من التجارب وانطلق خط أحمر التنبؤ الرياضي. الاتفاق بين هذين جيدة جدا. يمكنك أن ترى أن درجة حرارة التحقيق الأول تصل إلى 100 درجة بعد حوالي ثلاث دقائق ويبقى عند هذه الدرجة. سيتم قتل كل من البق هناك. ومع ذلك، فإن درجة الحرارة لجنة التحقيق الرابع يصل فقط 100 درجة بعد خمس دقائق. إذا كنت طهي الطعام الخاصة بك فقط لمدة ثلاث دقائق، ثم خارج ستكون (مخادعة) لطيفة والساخنة، ولكن من الداخل قد حصلت فقط على 60 درجة، وهذا يمكن أن يؤدي بسهولة إلى وضع خطير حيث البق لا يقتل. هذا هو السبب في أنك يجب أن يحرك الطعام بعد تسخينه في طنجرة الميكروويف لفترة من الزمن، ثم تسخينها مرة أخرى، للتأكد من أن جميع الأغذية يسخن بالتساوي.
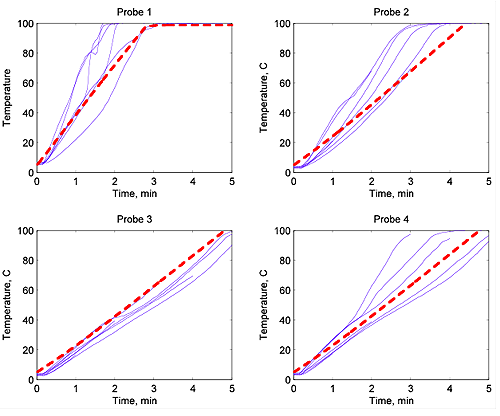
درجة حرارة الطعام مع مرور الوقت لمدة أربعة تحقيقات على أعماق متفاوتة. الخطوط الزرقاء تدل النتائج التجريبية وخطوط حمراء متقطع تظهر التوقعات الرياضية.
دقة التوقعات المذكورة أعلاه هي اختبارا مهما للنموذج الرياضي. أساسا أنها تظهر أن تقريبية حققنا معقولة. هذا ثم يعطينا الثقة لاستخدام نموذج لتفعل الكثير من "ماذا لو" الحسابات لمحاولة الخروج تصاميم مختلفة من فرن الميكروويف وتقييمها لقدرتها على طهي الطعام الآمن. وتبين أن الأفران مع النمام وضع أفضل بكثير من تلك التي مع القرص الدوار، وتلك التي لها تردد الفوضى لأفران ميكروويف هي أفضل للجميع.
الاستنتاجات
في هذا ومادة أخرى في هذه السلسلة، و تناول الطعام والشراب ومرح: مما يجعلها تنخفض بشكل جيد ، لقد إلا اليسير على سطح العديد من الطرق التي تستخدم الرياضيات في صناعة المواد الغذائية. وتشمل التطبيقات الأخرى استخدام الأساليب الإحصائية لضمان جودة الأغذية (في الواقع كان غينيس أن قدم للمرة الأولى الشهير اختبار t في الإحصاءات)، واستخدام أساليب التصوير لاختبار نضارة من المنتجات مثل الخبز والبسكويت، واستخدام ميكانيكا الموائع لتصميم العديد من الحلويات (يمكنك معرفة المزيد عن الرياضيات من التصوير في مقالتيإنقاذ الأرواح: رياضيات التصوير المقطعي ). رياضيات نقل الحرارة هي أيضا ذات أهمية حيوية في تصميم مرافق تخزين وإزالة الجليد عن الأغذية المجمدة، بحيث الطعام يبقى الطازجة وبالتالي آمنة. صناعة المواد الغذائية، وخاصة سلامة الغذاء، هي لهي حيث الرياضيات والرياضيات يمكن أن تقدم مساهمة كبيرة.
كفكرة النهائي، إذا كنت تريد أن ترى كيف الرياضيات يجيب على السؤال في غاية الاهمية لماذا المكسرات كبيرة في علبة الحبوب هي دائما في القمة، تحقق من العيش في عالم معقد الموقع.
حتى في تناول الطعام والشراب و التأكد من انها آمنة نستخدم الرياضيات
![حتى في تناول الطعام والشراب و التأكد من انها آمنة نستخدم الرياضيات]() Reviewed by . blogmathappily
on
5:00 م
Rating:
Reviewed by . blogmathappily
on
5:00 م
Rating:
