العمل مع الدعاة واللوغاريتمات

ما هو الأس؟

و الأس عدد يقول كم مرةلاستخدام رقم في الضرب. في هذا المثال: 2 3 = 2 × 2 × 2 = 8 (يتم استخدام 2 3 مرات في الضرب للحصول على 8)

ما هو لوغاريتم؟

A لوغاريتم يذهب في الاتجاه الآخر.

يسأل السؤال: "ما الأس أنتجت هذا؟":

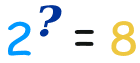
ويجيب على هذا النحو:

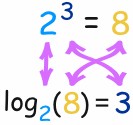
في هذا المثال:

• الأس يأخذ 2 و 3 ويعطي 8 (2، وتستخدم 3 مرات، ويضاعف إلى 8)
• لوغاريتم يأخذ 2 و 8 ويعطي 3 (2 يجعل 8 عندما تستخدم 3 مرات في الضرب)

يقول لوغاريتم كم من رقم واحد لمضاعفة للحصول على رقم آخر

لذلك اللوغاريتم يعطي في الواقع كنت الأس كما جوابه:

(انظر أيضا كيف الدعاة، الجذور واللوغاريتمات ترتبط).

العمل سويا

الأسس واللوغاريتمات تعمل معا بشكل جيد لأنهم "التراجع" بعضها البعض (ما دامت القاعدة "أ" هو نفسه):

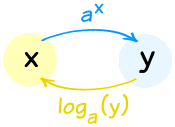
هم " وظائف عكسية "

فعل واحد، ثم من جهة أخرى، ويحصل لكم مرة أخرى إلى حيث كنت بدأت:

• القيام في ^العاشر ، ثم لوغاريتم، يعطيك س مرة أخرى:
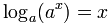
• القيام اللوغاريتم، ثم و ^العاشر ، ويتيح لك س مرة أخرى:

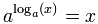
أنها سيئة للغاية أنها مكتوبة بشكل مختلف ... ويجعل الأمور تبدو غريبة.

لذلك قد تساعدك على التفكير و ^س ب "حتى" و تسجيل _و (خ) ب "القاعدة":

• الصعود، ثم إلى أسفل، يعود لك مرة أخرى: إلى أسفل (حتى (س)) = س ، و
• نزول، ثم يصل، يعود لك مرة أخرى: ما يصل (إلى أسفل (س)) = س

على أي حال، والشيء المهم هو أن:

وظيفة لوغاريتمي يمكن أن يكون "التراجع" من قبل الدالة الأسية.

(والعكس بالعكس)

كما في هذا المثال:

على سبيل المثال، ما هو العاشر في سجل ₃ (س) = 5

يمكننا استخدام الأس (مع وجود قاعدة 3) إلى "التراجع" لوغاريتم:

أبدا ب
نحن نريد أن "التراجع" سجل حتى نتمكن من الحصول على "س ="
استخدام الدالة الأسية (على كلا الجانبين!):
ونحن نعرف أن ، لذلك:		س = 3 5
إجابة:		س = 243

و أيضا:

مثال: حساب سنوي في ذ = تسجيل ₄ (1/4)

أبدا ب
استخدام الدالة الأسية على كلا الجانبين:
تبسيط:		4 ص = 1/4
الآن خدعة بسيطة: 1/4 = 4 -1
وبالتالي:		4 ص = 4 -1
و حينئذ:		ص = -1

خصائص اللوغاريتمات

واحدة من الأشياء قوية حول اللوغاريتمات هو أنها يمكن أن تتحول إلى ضرب الإضافة .

تسجيل الدخول _إلى (م × ن) = تسجيل _ل م + تسجيل _و ن

"سجل من الضرب هو مجموع السجلات"

لماذا هل هذا صحيح؟ انظر الحاشية .

استخدام هذا العقار و قوانين الدعاة نحصل على هذه الخصائص المفيدة:

تسجيل الدخول إلى (م × ن) = تسجيل ل م + تسجيل و ن	سجل من الضرب هو مجموع السجلات
تسجيل الدخول إلى (م / ن) = تسجيل ل م - تسجيلو ن	سجل للتقسيم هو الفرق من السجلات
تسجيل و (1 / ن) = -log على ن	هذا يلي فقط على من القاعدة السابقة "تقسيم"، ل تسجيل الدخول على (1) = 0
تسجيل الدخول إلى (م ص ) = ص (سجل ل م )	سجل للمتر مع ص ص الأس هو أضعاف سجل متر

تذكر: قاعدة "أ" هو نفسه دائما!

: التاريخ كانت اللوغاريتمات مفيدة جدا قبل أن يخترع الآلات الحاسبة ... على سبيل المثال، بدلا من ضرب  رقمين كبيرة، وذلك باستخدام اللوغاريتمات يمكن تحويلها إلى إضافة (أسهل بكثير!)

وكانت هناك كتب كاملة من الجداول لوغاريتم للمساعدة.

دعونا الحصول على بعض المتعة استخدامها:

مثال: تبسيط تسجيل _في ((س ² +1) ⁴ √x)

أبدا ب:		تسجيل الدخول إلى ((س 2 +1) 4 √x)
استخدام تسجيل و (بالمليون) = تسجيل ل م + تسجيل و ن :		تسجيل الدخول إلى ((س 2 +1) 4 ) + تسجيل و (√x)
استخدام تسجيل في (م ص ) = ص (سجل ل م) :		4 تسجيل و (س 2 +1) + تسجيل و (√x)
أيضا √x = س ½ :		4 تسجيل و (س 2 +1) + تسجيل و (خ ½ )
استخدام تسجيل في (م ص ) = ص (سجل ل م) مرة أخرى:		4 تسجيل و (س 2 +1) + ½ تسجيل في (خ)

هذا هو أقصى ما يمكننا تبسيط ذلك ... لا نستطيع أن نفعل أي شيء مع سجل _على (س ² +1) .

الجواب: 4 سجل _في (س ² +1) + ½ تسجيل _في (خ)

ملاحظة: لا توجد قاعدة للتعامل مع تسجيل _ل (م + ن) أو تسجيل _ل (م ن)

يمكننا أيضا تطبيق قواعد وغاريتم "إلى الوراء" على الجمع بين اللوغاريتمات:

مثال: تشغيل هذا في اللوغاريتم واحد: تسجيل الدخول _إلى (5) + تسجيل _في (خ) - سجل _ل (2)

أبدا ب:		تسجيل الدخول إلى (5) + تسجيل في (خ) - سجل ل (2)
استخدام تسجيل و (بالمليون) = تسجيل ل م + تسجيل و ن :		تسجيل الدخول إلى (5X) - سجل ل (2)
استخدام تسجيل في (م / ن) = تسجيل ل م - تسجيل و ن :		تسجيل الدخول إلى (5X / 2)

الجواب: تسجيل _ل (5X / 2)

وظائف لوغاريتم الطبيعي والأسي الطبيعية

عندما القاعدة هي ه ( " عدد أويلر " = 2.718281828459 ...) نحصل على:

• اللوغاريتم الطبيعي سجل _ه (خ)
  وهو أكثر شيوعا كتب قانون الجنسية(خ)
• الأسية الطبيعية وظيفة ه ^س

ونفس الفكرة يمكن للمرء أن "التراجع عن" الآخر لا يزال صحيحا:

قانون الجنسية (ه ^س ) = س

ه ^{(قانون الجنسية س)} = س

وهنا رسومهم البيانية:

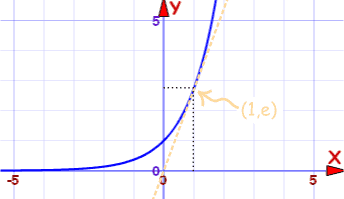
اللوغاريتم الطبيعي		الدالة الأسية الطبيعية
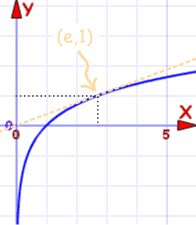الرسم البياني و (س) = LN(خ)		الرسم البياني و (س) = ه س
يمر عبر (1،0) و (ه، 1)		يمر عبر (0،1) و (1، ه)

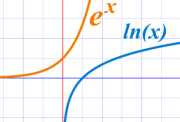
هم نفس المنحنى مع محور س و ص محور انقلبت .

الذي هو آخر شيء لتظهر لك ما هي وظائف عكسية.

على آلة حاسبة اللوغاريتم الطبيعي هو الزر "قانون الجنسية".

دائما في محاولة لاستخدام اللوغاريتمات الطبيعية والدالة الأسية الطبيعية كلما أمكن ذلك.

لوغاريتم المشتركة

عندما القاعدة هي 10 تحصل عليه:

لوغاريتم المشتركة تسجيل ₁₀ (خ) ، والذي هو مكتوب في بعض الأحيان كما سجل(خ)

المهندسين الحب لاستخدامه، ولكن لم يتم استخدامه كثيرا في الرياضيات.

على آلة حاسبة لوغاريتم المشتركة هو الزر "تسجيل". وهو مفيد لأنه يخبرك كيف "كبيرة" كان الرقم في العشرية (عدد المرات التي كنت بحاجة إلى استخدام 10 في الضرب).

مثال: حساب تسجيل ₁₀ 100

حسنا، 10 × 10 = 100، وذلك عندما يستخدم 10 2 مرات في الضرب تحصل على 100:

تسجيل ₁₀ 100 = 2

وبالمثل تسجيل ₁₀ 1000 = 3، تسجيل ₁₀ 10000 = 4، وهلم جرا.

مثال: حساب تسجيل ₁₀ 369

OK، الأفضل لاستخدام بلدي آلة حاسبة في "تسجيل" الزر:

تسجيل ₁₀ 369 = 2.567 ...

تغيير قاعدة

ماذا لو كنا نريد تغيير قاعدة لوغاريتم؟

سهل! مجرد استخدام هذه الصيغة:

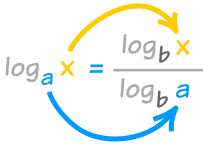
"س ترتفع وتنخفض"

أو طريقة أخرى للتفكير في الأمر هو أن سجل _ب و مثل "عامل التحويل" (نفس الصيغة على النحو الوارد أعلاه):

تسجيل الدخول _إلى س = سجل _ب س / سجل _ب ل

وحتى الآن يمكننا تحويل أي من القاعدة إلى أي قاعدة أخرى.

خاصية أخرى مفيدة هي:

تسجيل الدخول _إلى س = 1 / تسجيل _س ل

انظر كيف "س" و "" مواقف مقايضة؟

مثال: احسب 1 / سجل ₈ 2

1 / سجل ₈ 2 = تسجيل ₂ 8

و2 × 2 × 2 = 8، وذلك عندما يستخدم 2 3 مرات في الضرب تحصل 8:

1 / تسجيل ₈ 2 = سجل ₂ 8 = 3

ولكننا لا نستخدم اللوغاريتم الطبيعي في كثير من الأحيان، لذلك هذا هو الجدير بالذكر:

تسجيل الدخول _إلى س = LN س / من قانون الجنسية ل

مثال: حساب تسجيل ₄ 22

بلدي آلة حاسبة لايوجد " سجل 4 زر" ... ... ولكن لا يكون لها " قانون الجنسية " زر، حتى نتمكن من استخدام ما يلي:

تسجيل ₄ 22 = قانون الجنسية 22 / من قانون الجنسية 4 = 3.09 ... / 1.39 = 2.23 ... (إلى 2 عشرية)

ماذا تعني هذه الإجابة؟ وهذا يعني أن 4 مع الأس 2.23 يساوي 22. حتى نتمكن من التحقق من هذا الجواب:

تحقق: 4 ^2.23 = 22.01 (قريبة بما فيه الكفاية!)

هنا مثال آخر:

مثال: حساب تسجيل ₅ 125

تسجيل ₅ 125 = LN 125 / من قانون الجنسية 5 = 4.83 ... / 1.61 ... = 3 (بالضبط)

أنا أعلم أن 5 × 5 × 5 = 125، (5 يستخدم 3 مرات للحصول على 125)، لذلك كنت أتوقع جوابا من 3 ، وانها عملت!

ريال مدريد الاستخدام العالمي

وفيما يلي بعض الاستخدامات لوغاريتمات في العالم الحقيقي:

الزلازل

على أي زلزال هو مقياس لوغاريتمي.

و"مقياس ريختر" الشهير يستخدم هذه الصيغة:

M = تسجيل ₁₀ A + B

حيث A هي السعة (مم) يقاس رصد الزلازل
و B هو عامل تصحيح المسافة

في الوقت الحاضر هناك صيغ أكثر تعقيدا، لكنها لا تزال تستخدم مقياس لوغاريتمي.

صوت

يتم قياس جهارة في ديسيبل (ديسيبل قصيرة):

بريق في ديسيبل = 10 سجل ₁₀ (ع × 10 ¹² )

حيث ص هو ضغط الصوت.

الحمضية أو القلوية

يتم قياس الحموضة (أو القلوية) في درجة الحموضة:

الرقم الهيدروجيني = -log ₁₀ [H ⁺ ]

حيث H ⁺ هو التركيز المولي من أيونات الهيدروجين المنحل.
ملاحظة: في الكيمياء [] يعني تركيز المولي (الشامات للتر الواحد).

مزيد من الأمثلة

مثال: حل 2 سجل ₈ س = سجل ₈ 16

أبدا ب:		2 سجل 8 س = سجل 8 16
إحضار "2" في السجل:		تسجيل 8 س 2 = سجل 8 16
إزالة سجلات (التي هي نفس القاعدة):		س 2 = 16
حل:		س = -4 أو +4

ولكن ... ولكن ... ولكن ... لا يمكن أن يكون لها سجل رقما سالبا!

لذلك لم يتم تعريف -4 القضية.

الجواب: 4

تحقق: استخدام الآلة الحاسبة لمعرفة ما إذا كان هذا هو الجواب الصحيح ... أيضا محاولة "-4" القضية.

مثال: حل ه ^- ث ه = ^{2W + 6}

أبدا ب:		البريد -w ه = 2W + 6
تطبيق قانون الجنسية لكلا الجانبين:		قانون الجنسية (ه -w ) = من قانون الجنسية (ه 2W + 6 )
و قانون الجنسية (ه ث ) = ث :		-w = 2W + 6
تبسيط:		-3w = 6
حل:		ث = 6 / -3 = -2

الجواب: ث = - 2

التحقق من: ه ^{- (- 2)} = ه ² ه ^{2 (-2) +6} = ه ²

حاشية: لماذا سجل (م × ن) = السجل (م) + سجل (ن) ؟

لمعرفة لماذا ، سوف نستخدم 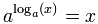و :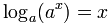

أولا، وجعل م و ن إلى "الدعاه لوغاريتمات":
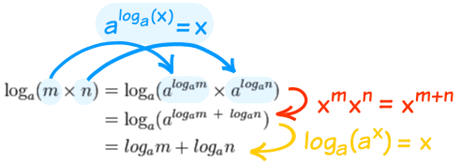	ثم استخدم إحدى قوانين الدعاة وأخيرا التراجع عن الأسس