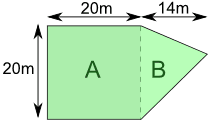
مساحات الأشكال

منطقة طائرة الأشكال

المنطقة هي حجم السطح!
معرفة المزيد حول منطقة ، أو محاولة لل منطقة حاسبة .

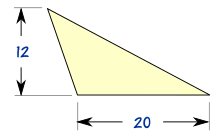
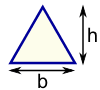	مثلث  منطقة = ½ × ب × ح ب = قاعدة ح = الارتفاع العمودي		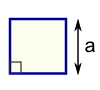	مربع  مساحة = من 2 إلى = طول الجانب
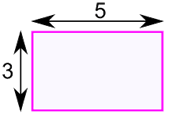
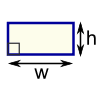	مستطيل  المساحة = ث × ح ث = العرض ح = ارتفاع		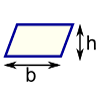	متوازي الاضلاع  المساحة = ب × ح ب = قاعدة ح = الارتفاع العمودي
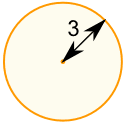
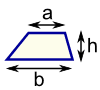	شبه منحرف (US)  شبه المنحرف (UK)  مساحة = ½ (أ + ب) × ح ح = الارتفاع العمودي			دائرة  المساحة = π × ص 2 محيط = 2 × π × ص ص = نصف قطرها
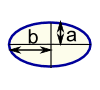	القطع الناقص  المساحة = π أب		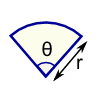	قطاع  المساحة = ½ × ص 2 × θ ص = نصف قطرها θ = زاوية في راديان

ملاحظة: ح هي في الزوايا ل ب: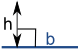

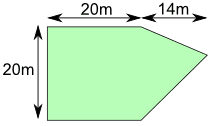
مثال: ما هي مساحة هذا المستطيل؟

الصيغة:

المساحة = ث × ح
ث = العرض
ح = ارتفاع

ونحن نعرف ث = 5 و ح = 3 ، لذلك:

المساحة = 5 × 3 = 15

مثال: ما هي مساحة هذه الدائرة؟

دائرة نصف قطرها = ص = 3

منطقة		= π × ص 2
		= π × 3 2
		= π × (3 × 3)
		= 3.14159 ... × 9
		= 28.27 (إلى 2 عشرية)

على سبيل المثال: ما هي مساحة هذا المثلث؟

ارتفاع = ح = 12

قاعدة = ب = 20

المساحة = ½ × ب × ح = ½ × 20 × 12 = 120

A أصعب سبيل المثال:

على سبيل المثال: سام يقطع العشب عند 0.10 $ للمتر المربع الواحد

وكم سام كسب قطع هذا المجال:

دعونا كسر المنطقة إلى قسمين:

الجزء (أ) هو مساحة:

منطقة A = A ² = 20M 20M × = 400M ²

الجزء B هو مثلث. ينظر جانبية أن لديها قاعدة من 20M وارتفاع 14M.

منطقة B = ½b × ح = ½ × 20M 14M × = 140M ²

وبالتالي فإن المساحة الكلية:

منطقة = مساحة المنطقة A + من B = 400M ² + 140M ² = 540M ²

سام يكسب 0.10 $ للمتر المربع الواحد

سام يكسب = $ 0.10 × 540M ² = $ 54