مقدمة في علم المثلثات

علم المثلثات (من trigonon اليونانية "مثلث" + METRON "التدبير")

تريد أن تتعلم علم المثلثات؟ وفيما يلي ملخص سريع.
اتبع الروابط لأكثر من ذلك، أو الذهاب إلى مؤشر علم المثلثات

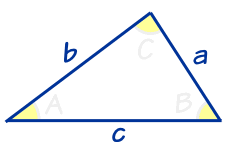علم المثلثات ... هو كل شيء عن مثلثات.

علم المثلثات يساعدنا على إيجاد الزوايا والمسافات، ويستخدم كثيرا في العلوم والهندسة، وألعاب الفيديو، وأكثر!

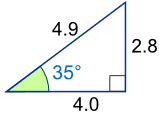
مثلث قائم الزاوية

المثلث الأكثر أهمية هو قائم الزاوية مثلث . ويظهر الزاوية اليمنى من مربع صغير في الزاوية:

وكثيرا ما وصفت زاوية أخرى θ ، وتسمى الاطراف الثلاثة ثم:

• مجاور : المجاورة (بجانب) زاوية θ
• المعاكس : مقابل زاوية θ
• والجانب الأطول هو الوتر

لماذا ا؟

لماذا هذا المثلث مهم جدا؟
تخيل أننا يمكن قياس طول وتصل ولكن نريد أن نعرف المسافة المباشرة وزاوية:

أو لدينا مسافة وزاوية وتحتاج إلى "مؤامرة نقطة" على طول وحتى:

مثل هذه الأسئلة شائعة في الهندسة، والرسوم المتحركة الكمبيوتر، وأكثر من ذلك.
وعلم المثلثات يعطي الأجوبة!

الجيب وجيب التمام والظل

وظائف رئيسية في حساب المثلثات و الجيب وجيب التمام والظل

هم ببساطة جانب واحد من مثلث قائم الزاوية مقسوما آخر.

للحصول على أي زاوية " θ ":

(غالبا ما يختصر الجيب وجيب التمام والظل إلى الخطيئة، كوس وتأن .)

على سبيل المثال: ما هو شرط من 35 درجة؟

باستخدام هذا المثلث (أطوال ليست سوى لمكان واحد عشري): الخطيئة (35 درجة) = مقابل / الوتر = 2.8 / 4.9 = 0.57 ...

الآلات الحاسبة لها الخطيئة، كوس وتأن، دعونا نرى كيفية استخدامها:

على سبيل المثال: ما هو ارتفاع المفقود هنا؟

• ونحن نعرف الوتر
• نريد أن نعرف مقابل

شرط هو نسبة مقابل / الوتر :

الخطيئة (45 درجة) = مقابل الوتر

الحصول على آلة حاسبة، واكتب في "45"، ثم اضغط على مفتاح "الخطيئة":

الخطيئة (45 درجة) = 0.7071 ...

ملاحظة: 0.7071 ... هي نسبة أطوال الأضلاع: وبعبارة أخرى فإن العكس هو 0.7071 ... مرات طالما  الوتر.
ربما يمكنك معرفة ذروة الآن؟
ولكن دعونا نفعل ذلك باستخدام رسميا بعض الجبر:

أبدا ب:		الخطيئة (45 درجة) = مقابل الوتر
ضع في ما نعرفه:		0.7071 ... = مقابل 20
الجانبين مبادلة:		مقابل 20 = 0.7071 ...
مضاعفة كلا الجانبين من 20 :		المعاكس = 0.7071 × 20 ...
حساب:		العكس = 14.14 (إلى 2 عشرية)

فعله!

محاولة الخطيئة كوس وتان

لعب مع هذا لبعض الوقت (تحريك الماوس حولها) وتعرف على قيم الجيب وجيب التمام والظل لزوايا مختلفة، مثل 0 °، 30 °، 45 °، 60 ° و 90 °.

أيضا محاولة 120 درجة، 135 درجة، 180 درجة، 240 درجة، 270 درجة وغيرها، وتلاحظ أن المواقف يمكن أن يكون إيجابيا أو سلبيا وفقا لقواعد الإحداثيات الديكارتية ، وبالتالي فإن التغيير الجيب وجيب التمام والظل بين الإيجابية والسلبية أيضا.

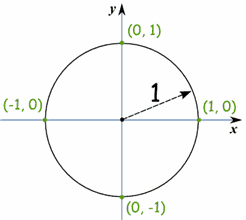
وحدة الدائرة

ما كنت لعبت فقط مع هو دائرة الوحدة .

وهي عبارة عن دائرة نصف قطرها 1 مع مركزها في 0.

لأن دائرة نصف قطرها 1، يمكننا قياس مباشرة الجيب وجيب التمام والظل.

وهنا نرى دالة الجيب التي تبذلها دائرة الوحدة:

© 2015 MathsIsFun.com ضد 0.81

والآن تعلمون لماذا علم المثلثات هو أيضا عن الدوائر !

ملاحظة: يمكنك ان ترى لطيفة الرسوم البيانية التي الجيب وجيب التمام والظل .

درجة وراديان

يمكن أن يكون الزوايا في الدرجات أو راديان . وهنا بعض الأمثلة:

زاوية	درجات	راديان
زاوية مستقيمة	90 °	π / 2
__ زاوية قائمة	180 °	π
دوران كامل	360 °	2 π

تكرار نمط

بسبب زاوية و يدور حولها وحول الدائرة وظائف الجيب وجيب التمام والظل كرر مرة واحدة كل دورة كاملة (انظر السعة، فترة، مرحلة التحول والتردد ).

عندما نريد لحساب وظيفة لزاوية أكبر من دورة كاملة 360 درجة (2 π راديان) طرحنا العديد من الدورات الكاملة حسب الحاجة لإعادته أقل من 360 درجة (2 π راديان):

على سبيل المثال: ما هو جيب التمام من 370 درجة؟

370 درجة أكبر من 360 درجة لذلك اسمحوا لنا طرح 360 °

370 ° - 360 ° = 10 °

كوس (370 درجة) = جتا (10 درجة) = 0.985 (إلى 3 منازل عشرية)

وعندما كانت الزاوية أقل من الصفر، فقط إضافة تناوب كاملة.

على سبيل المثال: ما هو جيب -3 راديان؟

-3 أقل من 0لذلك دعونا إضافة 2 π راديان

-3 + 2 π = -3 + 6.283 = 3.283 ... ... رادكونا

الخطيئة (-3) = الخطيئة (3،283 ...) = -0.141 (إلى 3 منازل عشرية)

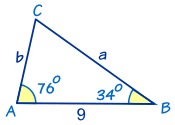
حل المثلثات

ويتمثل جزء كبير من علم المثلثات هو حل المثلثات . "حل" يعني إيجاد الجانبين والزوايا في عداد المفقودين.

مثال: العثور على زاوية مفقود "C"

زاوية C يمكن العثور عليها باستخدام زوايا المثلث إضافة إلى 180 درجة :

لذا C = 180 ° - 76 ° - 34 ° = 70 °

يمكن أن نجد أيضا أطوال الأضلاع في عداد المفقودين. والقاعدة العامة هي:

عندما نعرف أي 3 من الجانبين أو زوايا يمكننا العثور على 3 آخرين
(باستثناء حالة ثلاث زوايا)

رؤية حل المثلثات لمزيد من التفاصيل.

وظائف أخرى (ظل التمام، القاطع، قاطع التمام)

على غرار الجيب وجيب التمام والظل، وهناك ثلاثة أخرى الدوال المثلثية والتي تتم عن طريق تقسيم جانب واحد من جانب آخر:

وظيفة قاطع التمام:	ديوان الخدمة المدنية ( θ ) = الوتر / مقابل
القاطع وظيفة:	ثانية ( θ ) = الوتر / مجاور
وظيفة ظل التمام:	سرير ( θ ) = المتاخمة / مقابل

المثلثية والمثلث الهويات

وكما تحصل على نحو أفضل في علم المثلثات يمكنك ان تتعلم التالية:

	و الهويات المثلثية هي المعادلات التي تحققت لجميع المثلثات قائمة الزاوية .
	و الهويات المثلث هي المعادلات التي تحققت لجميع المثلثات (لا يكون لديك الزاوية اليمنى).