اللوغاريتمات 

كم عدد 2 الصورة لا ضربنا للحصول على 8 ؟

الجواب: 2 × 2 × 2 = 8 ، لذلك نحن بحاجة إلى مضاعفة 3 من 2 الصورة للحصول على 8

حتى اللوغاريتم هو 3

ونكتب "عدد 2S ضربنا للحصول على 8 هو 3 "، كما

سجل ₂ (8) = 3

حتى هذين الأمرين هي نفسها:

على سبيل المثال: ما هو سجل ₁₀ (100) ...؟

10 × 10 = 100

ضرب 2 10S معا يجعل 100، لذلك:

تسجيل ₁₀ (100) = 2

ملاحظة: استخدام الأس هو: 10 ² = 100

ولكن الآن نحن نسأل سؤالا جديدا:

على سبيل المثال: ما هو سجل ₁₀ (300) ...؟

10 × 10 = 100

10 × 10 × 10 = 1000

أوه لا! نحن إما منخفضة جدا أو مرتفعة جدا.

لذلك بضرب اثنين من 10S لا يكفي، ولكن بضرب ثلاثة 10S هو عدد كبير جدا من ...

... ولكن ماذا عن سنتين ونصف ...؟

نصف ضرب ...

كيف يمكننا أن نفعل نصف تتكاثر ؟

حسنا، نصف تتكاثر شيء يتعين علينا القيام به مرتين لجعل تتكاثر كله .

وهذا هو الجذر التربيعي !

√10 × √10 = 10

ضرب من قبل الجذر التربيعي هو مثل القيام نصف تتكاثر.

لذلك دعونا نحاول أن:

على سبيل المثال: تسجيل ₁₀ (300) (تابع)

حاول استخدام 10 في الضرب مرتين ونصف :

10 × 10 × √10
= 10 × 10 × 3.16 ...
= 316 ....

نحن قريبون من 300، ولذا فإننا يمكن أن نقول:

تسجيل ₁₀ (300) ≈ 2.5 (تقريبا)

وبعبارة أخرى باستخدام 10 في الضرب مرتين ونصف يحصل على ما يقرب من 300.
(ملاحظة: باستخدام الأسس نستطيع أن نقول 300 ≈ 10 ^2.5 )

وهذا ما يبدو على الرسم البياني:

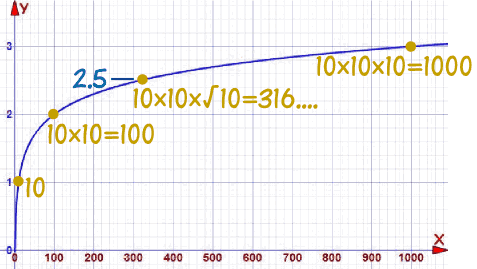
2: 10 × 10 = 100 
2.5: 10 × 10 × √10 = 316 .... 
3: 10 × 10 × 10 = 1000

حتى اللوغاريتمات ليست مجرد أرقام كاملة مثل 2 أو 3: وجدنا قيمة في 2.5 ،

يمكن أن نجد المزيد من القيم (باستخدام الجذور التكعيبية، القاعدة الرابعة الخ) مثل 2.75 أو 1.9055، وهلم جرا.

ولكن ليس لدينا لاستخدام الجذور التربيعية وغيرها لتجد اللوغاريتمات، وذلك لأن ...

... في الواقع هو أسهل لاستخدام آلة حاسبة!

مجرد استخدام حاسبة

على سبيل المثال على زر "تسجيل" سيعطي "القاعدة 10" اللوغاريتم.

مثال: استخدام الآلة الحاسبة، ما هو تسجيل ₁₀ (300) ؟

الحصول على آلة حاسبة، اكتب في 300 ، ثم اضغط سجل
الجواب: 2،477 ...

وهذا يعني أننا بحاجة إلى استخدام 10 في الضرب 2،477 ... مرات لجعل 300:

تسجيل ₁₀ (300) = 2.477 ...

تقديراتنا سابق من 2.5 لم يكن سيئا للغاية، كان ذلك؟
ملاحظة: استخدام الأس هو: 10 ^{2.477 ...} = 300

على سبيل المثال: ما هو تسجيل ₁₀ (640) ؟

الحصول على آلة حاسبة، اكتب في 640، ثم اضغط سجل
الجواب: 2،806 ...
وهذا يعني أننا بحاجة إلى استخدام 10 في الضرب 2،806 ... مرات لجعل 640:

تسجيل ₁₀ (640) = 2.806 ...

إلقاء نظرة على الرسم البياني أعلاه، ونرى ما هي القيمة التي تحصل عند x = 640
ملاحظة: استخدام الأس هو: 10 ^{2.806 ...} = 640