قوانيين النسب المثلثية

قوانيين النسب المثلثية 

${\ displaystyle (\ الخطيئة خ) ^ {2} + (\ كوس س) ^ {2} = 1}$

مجموع

${\ displaystyle {\ تبدأ {الانحياز} \ خطيئة \ اليسار (س + ص \ اليمين) و= \ الخطيئة س \ كوس ذ + \ كوس س \ الخطيئة ص، \ \\\ كوس غادر (س + ص \ اليمين) و= \ كوس س \ كوس Y- \ الخطيئة س \ الخطيئة ص، \ نهاية {الانحياز}}}$

فرق

${\ displaystyle {\ تبدأ {الانحياز} \ خطيئة \ اليسار (س ص \ اليمين) و= \ الخطيئة س \ كوس Y- \ كوس س \ الخطيئة ذ، \\\ كوس \ يقم (س ص \ اليمين) و= \ كوس العاشر \ كوس ذ + \ الخطيئة س \ الخطيئة ذ. \ نهاية {الانحياز}}}$

وهذه بدورها تؤدي إلى الصيغ الثلاث زاوية التالية:

${\ displaystyle {\ تبدأ {الانحياز} \ خطيئة \ اليسار (س + ص + Z \ اليمين) و= \ الخطيئة س \ كوس ذ \ كوس ض + \ الخطيئة ذ \ كوس ض \ كوس س + \ الخطيئة ض \ كوس كوس \ ص X- \ الخطيئة س \ الخطيئة ذ \ الخطيئة ض، \\\ كوس \ يقم (س + ص + Z \ اليمين) و= \ كوس س \ كوس ذ \ كوس Z- \ كوس س \ الخطيئة ذ \ الخطيئة Z- \ كوس ذ \ الخطيئة س \ الخطيئة Z- \ كوس ض \ الخطيئة س \ الخطيئة ص، \ نهاية {الانحياز}}}$

عندما تكون الزاويتين متساوية، الصيغ مبلغ تقلل إلى معادلات أبسط المعروفة باسم الصيغ مزدوجة الزاوية .

${\ displaystyle {\ تبدأ {الانحياز} \ خطيئة \ اليسار (2X \ اليمين) و= 2 \ الخطيئة س \ كوس س، \\\ كوس \ يقم (2X \ اليمين) و= \ كوس ^ {2} X- \ الخطيئة ^ {2} س = 2 \ كوس ^ {2} س 1 = 2/1 \ الخطيئة ^ {2} س. \ نهاية {الانحياز}}}$

عندما تكون ثلاث زوايا متساوية، الصيغ الثلاث زاوية تبسيط ل

${\ displaystyle {\ تبدأ {الانحياز} \ الخطيئة (3X) و= 3 \ الخطيئة س 4 \ الخطيئة ^ {3} س. \\\ كوس (3X) و= 4 \ كوس ^ {3} X-3 \ كوس س. \ نهاية {الانحياز}}}$

ويمكن أيضا أن هذه الهويات استخدامها للتوصل إلى هوية المنتج إلى المبلغ التي تم استخدامها في العصور القديمة لتحويل المنتج من رقمين إلى مبلغ من الأرقام وإلى حد كبير سرعة العمليات، مثل الكثير من دالة اللوغاريتم .

حساب التفاضل والتكامل ]

ل التكاملات و مشتقات الدوال المثلثية، راجع الأقسام ذات الصلة من تمايز الدوال المثلثية ، قوائم من التكامل و قائمة تكاملات الدوال المثلثية . وفيما يلي قائمة من المشتقات والتكامل من ستة الدوال المثلثية الأساسية. عدد  C هو ثابت التكامل.

${\ displaystyle {\ تبدأ {مجموعة} {| ص | ص ص |} و (خ) & F '(س) و \ كثافة و (خ) \، DX \\\ hline \ الخطيئة العاشر و\ كوس العاشر و- \ كوس س + C \\\ كوس العاشر و- \ الخطيئة العاشر و\ الخطيئة س + C \\\ تان س و \ ثانية ^ {2} س = 1 + \ تان ^ {2} س و- \ قانون الجنسية \ ترك | \ كوس س \ الحق | + C \\\ سرير العاشر و- \ ديوان الخدمة المدنية ^ {2} س = - (1+ \ سرير ^ {2} خ) و \ قانون الجنسية \ يسار | الخطيئة س \ اليمين \ | + C \\\ ثانية س و \ ثانية س \ تان س و \ قانون الجنسية \ ترك | \ ثانية س + \ تان س \ الحق | + C \\\ ديوان الخدمة المدنية العاشر و- \ ديوان الخدمة المدنية س \ سرير العاشر و- \ قانون الجنسية \ ترك | \ ديوان الخدمة المدنية س + \ سرير س \ الحق | + C \ نهاية { مجموعة مصفوفة}}}$

التعاريف باستخدام معادلات وظيفية  

في التحليل الرياضي ، يمكن للمرء تحديد الدوال المثلثية باستخدام المعادلات الوظيفية على أساس الخصائص مثل الصيغة الفرق. أخذ على النحو الوارد هذه الصيغ، يمكن للمرء أن يثبت أن اثنين فقط من وظائف حقيقية تلبي هذه الشروط. رمزيا، ونحن نقول ان هناك بالضبط زوج واحد من وظائف حقيقية - الخطيئة وكوس - مثل للجميع ان الارقام الحقيقية س و ذ ، يحمل المعادلة التالية: ^[14]

${\ displaystyle \ كوس (س ص) = \ كوس س \ كوس ذ + \ الخطيئة س \ الخطيئة ذ \}$

مع شرط أضاف أن

${\ displaystyle 0 <س \ كوس خ <\ الخطيئة س <س {\ HBOX {ل}} 0 <س <1. \}$

الاشتقاقات الأخرى، بدءا من المعادلات الفنية الأخرى، هي أيضا ممكن، ويمكن تمديد هذه الاشتقاقات إلى الأعداد المركبة. وكمثال على ذلك، وهذا الاشتقاق يمكن استخدامها لتحديد حساب المثلثات في مجالات جالويس .

حساب  

لحساب الدوال المثلثية هو موضوع معقد، والتي يمكن تجنبها اليوم من قبل معظم الناس بسبب توفر نطاق واسع من أجهزة الكمبيوتر و الآلات الحاسبة العلمية التي توفر المدمج في الدوال المثلثية للأي زاوية. هذا القسم، ومع ذلك، يصف تفاصيل حساب في ثلاثة سياقات مهمة، وهي أن الاستخدام التاريخي للجداول مثلثية، والتقنيات الحديثة التي تستخدمها أجهزة الكمبيوتر، وعدد قليل من زوايا "مهمة" حيث تم العثور على قيم الدقيق بسيطة بسهولة.

الخطوة الأولى في حساب أي وظيفة المثلثية هي مجموعة من زاوية معينة إلى "انخفاض زاوية" داخل مجموعة صغيرة من زوايا تخفيض الحد، ويقول ل0 π/2 ، وذلك باستخدام تواترها والتماثلات من الدوال المثلثية.

المقال الرئيسي: توليد الجداول المثلثية

قبل أجهزة الكمبيوتر، والناس عادة تقييم الدوال المثلثية من التحريف من جدول مفصل من قيمها، وتحسب للعديد من الشخصيات الهامة . كانت هذه الجداول المتاحة لطالما تم وصفها الدوال المثلثية (انظر التاريخ أدناه)، وتم إنشاؤها عادة من خلال تطبيق المتكررة من زاوية نصف وزاوية بالإضافة الهويات بدءا من قيمة معروفة (مثل الخطيئة ( π/2 ) =  1).

استخدام أجهزة الكمبيوتر الحديثة مجموعة متنوعة من التقنيات. ^[15] طريقة واحد مشترك، وخاصة على معالجات أعلى نهاية مع النقطة العائمة وحدة، هو الجمع بين متعدد الحدود أو عقلاني تقريب (مثل تشيبيشيف التقريب ، وتقريب أفضل موحد، و Padé التقريب ، وعادة لتوضيحات أعلى أو متغيرة، تايلور و سلسلة لوران ) مع تخفيض نطاق و بحث جدول -أنهم ننظر أولا في أقرب زاوية في طاولة صغيرة، ومن ثم استخدام متعدد الحدود لحساب التصحيح. ^[16] الأجهزة التي تفتقر إلى مضاعفات الأجهزة غالبا  ما تستخدم خوارزمية دعا CORDIC (وكذلك التقنيات ذات الصلة)، والذي يستخدم الوحيد الجمع والطرح و bitshift ، و بحث الجدول . وتنفذ هذه الأساليب عادة في الأجهزة وحدة الفاصلة العائمة لأسباب تتعلق بالأداء.

لإجراء العمليات الحسابية بدقة عالية جدا، وعندما يصبح توسع سلسلة التقارب بطيئة جدا، الدوال المثلثية يمكن أن يقترب من المتوسط الحسابي-الهندسي ، والتي هي نفسها يقترب من وظيفة المثلثية من قبل ( مجمع ) بيضاوي الشكل لا يتجزأ . ^[17]

المقال الرئيسي: الثوابت المثلثية بالضبط

وأخيرا، بالنسبة لبعض زوايا بسيطة، والقيم يمكن حسابها بسهولة باليد باستخدام نظرية فيثاغورس ، كما في الأمثلة التالية. على سبيل المثال، الجيب وجيب التمام والظل من أي عدد صحيح متعددة من π/60 راديان (3 درجات) ويمكن الاطلاع بالضبط باليد .

النظر في مثلث قائم الزاوية حيث اثنين من زوايا أخرى على قدم المساواة، وبالتالي فهي على حد سواء π/4 راديان (45 درجة). ثم طول الجانب ب وطول الجانب من متساوون. نستطيع أن نختار ل = ب = 1 . قيم الجيب وجيب التمام والظل من زاوية π/4ويمكن بعد ذلك وجدت راديان (455 درجة) باستخدام نظرية فيثاغورس:

${\ displaystyle ج = {\ الجذر التربيعي {و^ {2} + ب ^ {2}}} = {\ الجذر التربيعي {2}} \،.}$

وبالتالي:

${\ displaystyle \ الخطيئة {\ فارك {\ بي} {4}} = \ خطيئة 45 ^ {\ CIRC} = \ كوس {\ فارك {\ بي} {4}} = \ كوس 45 ^ {\ CIRC} = { 1 \ على {\ الجذر التربيعي {2}}} = {{\ الجذر التربيعي {2}} \ أكثر من 2}، \}$

${\ displaystyle \ تان {\ فارك {\ بي} {4}} = \ تان 45 ^ {\ CIRC} = {{\ الخطيئة {\ فارك {\ بي} {4}}} \ على {\ كوس {\ فارك {\ بي} {4}}}} = {1 \ على {\ الجذر التربيعي {2}}} \ cdot {{\ الجذر التربيعي {2}} \ أكثر من 1} = {{\ الجذر التربيعي {2}} \ على {\ الجذر التربيعي {2}}} = 1. \}$

حساب الدوال المثلثية من مثلث متساوي الأضلاع

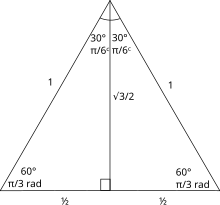
لتحديد الدوال المثلثية للزوايا π/3 راديان (60 درجة) و π/6 راديان (30 درجة)، ونحن نبدأ مع مثلث متساوي الأضلاع طول الجانب 1. جميع زواياه هي π/3 راديان (60 درجة). بتقسيمه إلى قسمين، نحصل على مثلث قائم الزاوية مع π/6 راديان (30 درجة) و π/3 راديان (60 درجة) الزوايا. لهذا المثلث، وعلى الجانب أقصر هو 1/2 ، وهو أكبر الجانب التالي √ 3/2 والوتر هو 11. هذه المحاصيل:

${\ displaystyle \ الخطيئة {\ فارك {\ بي} {6}} = \ خطيئة 30 ^ {\ CIRC} = \ كوس {\ فارك {\ بي} {3}} = \ كوس 60 ^ {\ CIRC} = { 1 \ أكثر من 2} \ ،،}$

${\ displaystyle \ كوس {\ فارك {\ بي} {6}} = \ كوس 30 ^ {\ CIRC} = \ الخطيئة {\ فارك {\ بي} {3}} = \ خطيئة 60 ^ {\ CIRC} = { {\ الجذر التربيعي {3}} \ أكثر من 2} \ ،،}$

${\ displaystyle \ تان {\ فارك {\ بي} {6}} = \ تان 30 ^ {\ CIRC} = \ سرير {\ فارك {\ بي} {3}} = \ سرير 60 ^ {\ CIRC} = { 1 \ على {\ الجذر التربيعي {3}}} = {{\ الجذر التربيعي {3}} \ أكثر من 3} \،.}$

القيم الخاصة في الدوال المثلثية  ]

هناك بعض القيم الخاصة التي تستخدم عادة في الدوال المثلثية، كما هو مبين في الجدول التالي.

${\ displaystyle {\ تبدأ {مجموعة} {| ج | cccccccc |} {\ تبدأ {مصفوفة} {\ النص {راديان}} \\ {\ النص {درجة}} \ نهاية {مصفوفة}} و {\ تبدأ {مصفوفة } 0 \\ 0 ^ {\ CIRC} \ نهاية {مصفوفة}} و {\ تبدأ {مصفوفة} {\ فارك {\ بي} {12}} \\ 15 ^ {\ CIRC} \ نهاية {مصفوفة}} و { \ تبدأ {مصفوفة} {\ فارك {\ بي} {8}} \\ 22.5 ^ {\ CIRC} \ نهاية {مصفوفة}} و {\ تبدأ {مصفوفة} {\ فارك {\ بي} {6}} \\ 30 ^ {\ CIRC} \ نهاية {مصفوفة}} و {\ تبدأ {مصفوفة} {\ فارك {\ بي} {4}} \\ 45 ^ {\ CIRC} \ نهاية {مصفوفة}} و {\ تبدأ {مصفوفة } {\ فارك {\ بي} {3}} \\ 60 ^ {\ CIRC} \ نهاية {مصفوفة}} و {\ تبدأ {مصفوفة} {\ فارك {5 \ بي} {12}} \\ 75 ^ { \ CIRC} \ نهاية {مصفوفة}} و {\ تبدأ {مصفوفة} {\ فارك {\ بي} {2}} \\ 90 ^ {\ CIRC} \ نهاية {مصفوفة}} \\\ hline \ الخطيئة & 0 & {\ فارك {{\ الجذر التربيعي {6}} - {\ الجذر التربيعي {2}}} {4}} و {\ فارك {\ الجذر التربيعي {2 - {\ الجذر التربيعي {2}}}} {2}} و {\ فارك { 1} {2}} و {\ فارك {\ الجذر التربيعي {2}} {2}} و {\ فارك {\ الجذر التربيعي {3}} {2}} و {\ فارك {{\ الجذر التربيعي {6}} + { \ الجذر التربيعي {2}}} {4}} & 1 \\\ كوس & 1 & {\ فارك {{\ الجذر التربيعي {6}} + {\ الجذر التربيعي {2}}} {4}} و {\ فارك {\ الجذر التربيعي {2 + {\ الجذر التربيعي {2}}}} {2}} و {\ فارك {\ الجذر التربيعي {3}} {2}} و {\ فارك {\ الجذر التربيعي {2}} {2}} و {\ فارك {1 } {2}} و {\ فارك {{\ الجذر التربيعي {6}} - {\ الجذر التربيعي {2}}} {4}} & 0 \\\ تان & 0 & 2 - {\ الجذر التربيعي {3}} و {\ الجذر التربيعي {2 }} - 1 و {\ فارك {\ الجذر التربيعي {3}} {3}} & 1 & {\ SQR$ ر {3}} & 2 + {\ الجذر التربيعي {3}} & \ infty \\\ سرير و\ infty & 2 + {\ الجذر التربيعي {3}} و {\ الجذر التربيعي {2}} + 1 & {\ الجذر التربيعي {3}} & 1 & { \ فارك {\ الجذر التربيعي {3}} {3}} و 2 - {\ الجذر التربيعي {3}} & 0 \\\ ثانية & 1 & {\ الجذر التربيعي {6}} - {\ الجذر التربيعي {2}} و {\ الجذر التربيعي {2} } {\ الجذر التربيعي {2 - {\ الجذر التربيعي {2}}}} & {\ فارك {2 {\ الجذر التربيعي {3}}} {3}} و {\ الجذر التربيعي {2}} و 2 و {\ الجذر التربيعي {6}} + {\ الجذر التربيعي {2}} & \ infty \\\ ديوان الخدمة المدنية و\ infty و{\ الجذر التربيعي {6}} + {\ الجذر التربيعي {2}} و {\ الجذر التربيعي {2}} {\ الجذر التربيعي {2 + {\ الجذر التربيعي {2}}}} و 2 و {\ الجذر التربيعي {2}} و {\ فارك {2 {\ الجذر التربيعي {3}}} {3}} و {\ الجذر التربيعي {6}} - {\ الجذر التربيعي {2}} & 1 \\\ نهاية {مجموعة}}}^[18]

الرمز ∞ هنا يمثل نقطة اللانهاية على الخط الحقيقي بمد إسقاطي ، والحد على الخط الحقيقي الموسعة هو + ∞ على جانب واحد و -∞ من جهة أخرى.

الدوال العكسية  ]

المقال الرئيسي: الدوال المثلثية العكسية

الدوال المثلثية هي دورية، وبالتالي لا injective ، لذلك بدقة أنهم لم يكن لديك وظيفة عكسية . لذلك، لتحديد وظيفة عكسية علينا أن تقييد المجالات الخاصة بهم حتى أن وظيفة المثلثية هي bijective . في ما يلي، والمهام على اليسار المحدد من قبل المعادلة على اليمين. هذه ليست هويات تثبت. يتم تعريف العكوس الرئيسية عادة على النحو التالي:

${\ displaystyle {\ تبدأ {مجموعة} {RRC} {\ النص {وظيفة}} و {\ النص {تعريف}} و {\ النص {الميدان القيمة}} \\\ hline \ جيب الزاوية القوسي س = ص و\ الخطيئة ص = س & - {\ فارك {\ بي} {2}} \ LEQ ذ \ LEQ {\ فارك {\ بي} {2}} \\\ قوس جيب تمام الزاوية س = ص و\ كوس = ذ س & 0 \ LEQ ذ \ LEQ \ بي \\\ ظل الزاوية القوسي س = ص و\ تان ص = س و- {\ فارك {\ بي} {2}} <ص <{\ فارك {\ بي} {2}} \\\ operatorname {arccot} س = ص و\ سرير ص = س و 0 <ص <\ بي \\\ operatorname {arcsec} س = ص و\ ثانية ص = س و 0 \ LEQ ذ \ LEQ \ بي، \، ص \ neq {\ فارك {\ بي} {2}} \\\ operatorname {arccsc } س = ص و\ ديوان الخدمة المدنية ص = س و- {\ فارك {\ بي} {2}} \ LEQ ذ \ LEQ {\ فارك {\ بي} {2}}، \، ص \ neq 0 \ نهاية {مجموعة}} }$