مقدمة في اللوغاريتمات

في شكله أبسط، واللوغاريتم يجيب على السؤال:

كم رقم واحد لا ضربنا للحصول على رقم آخر؟

مثال: كم عدد 2 الصورة لا ضربنا للحصول على 8 ؟

الجواب: 2 × 2 × 2 = 8 ، لذلك كان علينا أن تتضاعف 3 من 2 الصورة للحصول على 8

حتى اللوغاريتم هو 3

كيفية كتابة ذلك

نكتب "عدد 2S نحن بحاجة إلى مضاعفة للحصول على 8 هو 3" على النحو التالي:

سجل ₂ (8) = 3

حتى هذين الأمرين هي نفسها:

عدد أننا تتضاعف يسمى "القاعدة"، لذلك نستطيع أن نقول:

• "لوغاريتم (8) مع قاعدة 2 هو 3"
• أو "تسجيل قاعدة 2 من 8 هو 3"
• أو "سجل قاعدة 2 من 8 هو 3"

لاحظ أننا نتعامل مع ثلاثة أرقام:

• على قاعدة : عدد أننا بضرب (أ "2" في المثال أعلاه)
• كم مرة لاستخدامها في الضرب (3 مرات، وهو اللوغاريتم )
• عدد نريد أن نحصل على (و"8")

مزيد من الأمثلة

على سبيل المثال: ما هو سجل ₅ (625) ...؟

ما نطلبه "كم 5S بحاجة إلى أن تتضاعف معا للحصول على 625؟"
5 × 5 × 5 × 5 = 625 ، لذلك نحن بحاجة 4 من 5S
الجواب: تسجيل ₅ (625) = 4

على سبيل المثال: ما هو سجل ₂ (64) ...؟

ما نطلبه "كم 2S بحاجة إلى أن تتضاعف معا للحصول على 64؟"
2 × 2 × 2 × 2 × 2 × 2 = 64 ، لذلك نحن بحاجة 6 من 2S
الجواب: تسجيل ₂ (64) = 6

الأس

الأسس واللوغاريتمات هي ذات الصلة، دعونا معرفة كيف ...

و الأس يقول كم مرة لاستخدام رقم في الضرب. في هذا المثال: 2 3 = 2 × 2 × 2 = 8 (يتم استخدام 2 3 مرات في الضرب للحصول على 8)

لذلك اللوغاريتم يجيب على سؤال مثل هذا:

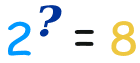
في هذا الطريق:

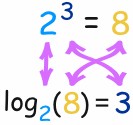
لوغاريتم يقول لنا ما هو الأس!

في هذا المثال "القاعدة" هي 2 و "الأس" هو 3:

لذلك لوغاريتم يجيب على السؤال:

ما الأس نحتاج 
(لرقم واحد ليصبح عدد آخر) ؟

في العام القضية هي:

على سبيل المثال: ما هو سجل ₁₀ (100) ...؟

10 ² = 100

لذلك فإن الأس 2 هو مطلوب لجعل 10 إلى 100، و:

تسجيل ₁₀ (100) = 2

على سبيل المثال: ما هو سجل ₃ (81) ...؟

3 ⁴ = 81

لذلك فإن الأس 4 هو مطلوب لجعل 3 إلى 81، و:

تسجيل ₃ (81) = 4

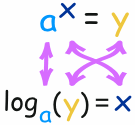
اللوغاريتمات المشتركة: قاعدة 10

في بعض الأحيان يتم كتابة اللوغاريتم دون قاعدة، مثل هذا:

تسجيل (100)

هذا عادة ما يعني أن القاعدة هي حقا 10 .

ومن دعا إلى "اللوغاريتم المشترك". المهندسين الحب لاستخدامها.

على الآلة الحاسبة هو زر "تسجيل".

ومن كم مرة نحن بحاجة إلى استخدام 10 في الضرب، للحصول على العدد المطلوب لدينا.

على سبيل المثال: تسجيل (1000) = تسجيل ₁₀ (1000) = 3

اللوغاريتمات الطبيعية: قاعدة "ه"

قاعدة أخرى التي كثيرا ما تستخدم ل ه (عدد أويلر) وهي عبارة عن 2.71828.

وهذا ما يسمى "اللوغاريتم الطبيعي". علماء الرياضيات استخدام هذه واحدة الكثير.

على الآلة الحاسبة هو زر "قانون الجنسية".

ومن كم مرة نحن بحاجة إلى استخدام "البريد" في الضرب، للحصول على العدد المطلوب لدينا.

مثال: قانون الجنسية (7،389) = تسجيل _البريد ( 7،389 ) ≈ 2

لأن 2.71828 ² ≈ 7.389

ولكن في بعض الأحيان هناك التباس ...!

استخدام الرياضيات "تسجيل" (بدلا من "قانون الجنسية") للدلالة على اللوغاريتم الطبيعي. هذا يمكن أن يؤدي إلى الارتباك:

مثال	يفكر المهندس	يعتقد الرياضيات
تسجيل (50)	تسجيل 10 (50)	تسجيل البريد (50)	ارتباك
قانون الجنسية (50)	تسجيل البريد (50)	تسجيل البريد (50)	أي التباس
تسجيل 10 (50)	تسجيل 10 (50)	تسجيل 10 (50)	أي التباس

لذلك، يجب الحرص عند قراءة "تسجيل" عليك أن تعرف ما تعنيه قاعدة!

اللوغاريتمات يمكن أن يكون الكسور العشرية

استخدمت كل من الأمثلة لدينا اللوغاريتمات عدد بأكملها (مثل 2 أو 3)، ولكن يمكن اللوغاريتمات لديها قيم عشرية مثل 2.5، أو 6.081، الخ

على سبيل المثال: ما هو سجل ₁₀ (26) ...؟

الحصول على آلة حاسبة، اكتب في 26 ثم اضغط على سجل الجواب: 1.41497 ...

لوغاريتم يقول ان 10 ^{1.41497 ...} = 26
(10 مع الأس من 1.41497 ... يساوي 26)

وهذا هو ما يبدو على الرسم البياني: نرى كيف لطيف وسلس الخط.

قراءة اللوغاريتمات يمكن أن يكون لها الكسور العشرية لمعرفة المزيد.

اللوغاريتمات السلبية

-	نفي؟ لكن اللوغاريتمات التعامل مع التكاثر. ما هو عكس التكاثر؟ الفاصل!

A اللوغاريتم السلبي يعني كم مرة لتقسيم من قبل عدد.

فإننا يمكن أن يكون الانقسام واحد فقط:

على سبيل المثال: ما هو سجل ₈ (0.125) ...؟
حسنا، 1 ÷ 8 = 0.125 ،
حتى تسجيل ₈ (0.125) = -1

أو العديد من الانقسامات:

على سبيل المثال: ما هو سجل ₅ (0.008) ...؟
1 ÷ 5 ÷ 5 ÷ 5 = 5 ^-3 ،
حتى تسجيل ₅ (0.008) = -3

كل ذلك من المنطقي

التكاثر وتقسيم جميعا جزء من نفس النمط البسيط.

دعونا نلقي نظرة على بعض BASE-10 اللوغاريتمات كمثال:

	رقم	كم عدد 10S	قاعدة 10 لوغاريتم
	.. الخ ..
	1000	1 × 10 × 10 × 10	تسجيل 10 (1000)	= 3
	100	1 × 10 × 10	تسجيل 10 (100)	= 2
	10	1 × 10	تسجيل 10 (10)	= 1
	1	1	تسجيل 10 (1)	= 0
	0.1	1 ÷ 10	تسجيل 10 (0.1)	= -1
	0.01	1 ÷ 10 ÷ 10	تسجيل 10 (0.01)	= -2
	0.001	1 ÷ 10 ÷ 10 ÷ 10	تسجيل 10 (0،001)	= -3
	.. الخ ..