العلاقة بين العدد 1 والنسب المثلثية

العلاقة بين العدد 1  والنسب المثلثية 

 

  

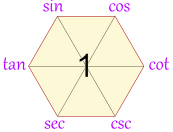Clockwise

tan(x) = sin(x) / cos(x) sin(x) = cos(x) / cot(x) cos(x) = cot(x) / csc(x) cot(x) = csc(x) / sec(x) csc(x) = sec(x) / tan(x) sec(x) = tan(x) / sin(x)

Counterclockwise

cos(x) = sin(x) / tan(x) sin(x) = tan(x) / sec(x) tan(x) = sec(x) / csc(x) sec(x) = csc(x) / cot(x) csc(x) = cot(x) / cos(x) cot(x) = cos(x) / sin(x)

Product Identities

The hexagon also shows that a function between any two functions is equal to them multiplied together (if they are opposite each other, then the "1" is between them):

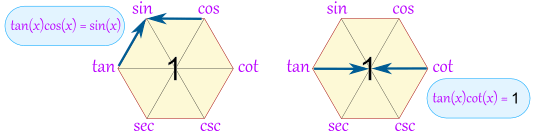Example: tan(x)cos(x) = sin(x)	Example: tan(x)cot(x) = 1

Some more examples:

• sin(x)csc(x) = 1
• tan(x)csc(x) = sec(x)
• sin(x)sec(x) = tan(x)

 

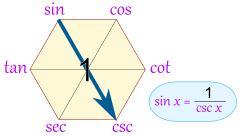Here you can see that sin(x) = 1 / csc(x)

Here is the full set:

• sin(x) = 1 / csc(x)
• cos(x) = 1 / sec(x)
• cot(x) = 1 / tan(x)
• csc(x) = 1 / sin(x)
• sec(x) = 1 / cos(x)
• tan(x) = 1 / cot(x)

Bonus!

AND we also get these:

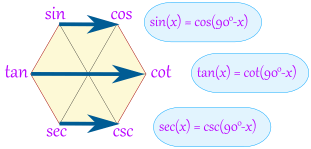
Examples:

• sin(30°) = cos(60°)
• tan(80°) = cot(10°)
• sec(40°) = csc(50°)

Double Bonus: The Pythagorean Identities

The Unit Circle shows us that

sin² x + cos² x = 1

The magic hexagon can help us remember that, too, by going clockwise around any of these three triangles:

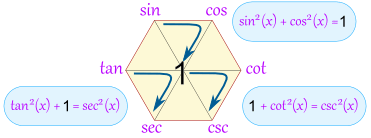
And we have:

• sin²(x) + cos²(x) = 1
• 1 + cot²(x) = csc²(x)
• tan²(x) + 1 = sec²(x)

You can also travel counterclockwise around a triangle, for example:

• 1 - cos²(x) = sin²(x)