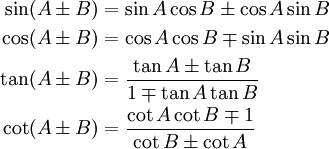قوانيين النسب المثلثية
قوانيين النسب المثلثية قوانيين النسب المثلثية

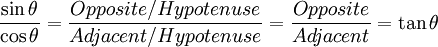


Sine Function:
| sin(θ) = Opposite / Hypotenuse |
Cosine Function:
| cos(θ) = Adjacent / Hypotenuse |
Tangent Function:
| tan(θ) = Opposite / Adjacent |
For a given angle θ each ratio stays the same
no matter how big or small the triangle is
no matter how big or small the triangle is
When we divide Sine by Cosine we get:
So we can say:
tan(θ) = sin(θ)/cos(θ)
That is our first Trigonometric Identity.
Cosecant, Secant and Cotangent
We can also divide "the other way around" (such as Adjacent/Opposite instead of Opposite/Adjacent):

Cosecant Function:
| csc(θ) = Hypotenuse / Opposite |
Secant Function:
| sec(θ) = Hypotenuse / Adjacent |
Cotangent Function:
| cot(θ) = Adjacent / Opposite |
Because of all that we can say:
sin(θ) = 1/csc(θ)
cos(θ) = 1/sec(θ)
tan(θ) = 1/cot(θ)
And the other way around:
csc(θ) = 1/sin(θ)
sec(θ) = 1/cos(θ)
cot(θ) = 1/tan(θ)
And we also have:
cot(θ) = cos(θ)/sin(θ)
Pythagoras Theorem
For the next trigonometric identities we start with Pythagoras' Theorem:
 |
The Pythagorean Theorem says that, in a right triangle, the square of a plus the square of b is equal to the square of c:
a2 + b2 = c2
|
Dividing through by c2 gives
a2c2 = b2c2 = c2c2
This can be simplified to:
(ac)2 + (bc)2 = 1
Now, a/c is Opposite / Hypotenuse, which is sin(θ)
And b/c is Adjacent / Hypotenuse, which is cos(θ)
So (a/c)2 + (b/c)2 = 1 can also be written:
sin2 θ + cos2 θ = 1
Note:
- sin2 θ means to find the sine of θ, then square the result, and
- sin θ2 means to square θ, then do the sine function
Related identities include:
sin2 θ = 1 − cos2 θ
cos2 θ = 1 − sin2 θ
tan2 θ + 1 = sec2 θ
tan2 θ = sec2 θ − 1
cot2 θ + 1 = csc2 θ
cot2 θ = csc2 θ − 1
cos2 θ = 1 − sin2 θ
tan2 θ + 1 = sec2 θ
tan2 θ = sec2 θ − 1
cot2 θ + 1 = csc2 θ
cot2 θ = csc2 θ − 1
How Do You Remember Them?
The identities mentioned so far can be remembered
using one clever diagram called the Magic Hexagon: | 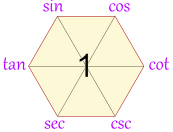 |
But Wait ... There is More!
There are many more identities ... here are some of the more useful ones:
Opposite Angle Identities
sin(−θ) = −sin(θ)
cos(−θ) = cos(θ)
tan(−θ) = −tan(θ)
Double Angle Identities
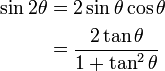 |
 |
sin(−θ) = −sin(θ)
cos(−θ) = cos(θ)
tan(−θ) = −tan(θ)
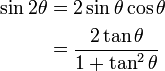 |
 |
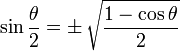 |
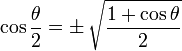 |
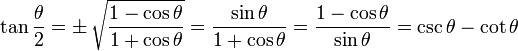 |
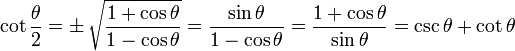 |
قوانيين النسب المثلثية
![قوانيين النسب المثلثية]() Reviewed by . blogmathappily
on
2:24 م
Rating:
Reviewed by . blogmathappily
on
2:24 م
Rating: